NP 완전 문제
| NP | 어떤 결정 문제의 답이 YES일 때 그 문제의 답이 YES라는 것을 입증하는 힌트가 주어지면 그 힌트를 사용해서 그 문제으 ㅣ답이 정말 YES라는 것을 다항식 시간 이내에 확인 할 수 있는 문제이다. |
| NP-난해 문제 | 적어도 NP 문제보다는 어려우며 모든 NP 문제를 다항식 시간 내에 어떤 문제로 환원(Reduction) 할 수 있는 경우 그 문제는 NP-난해 문제라고 하며 NP-난해 문제를 다항식 시간 내에 풀 수 있으면 모든 NP 문제를 다항식 시간 내에 풀 수 있다. |
| NP 완전 문제 | NP-난해 문제에도 포함되며 NP 문제에도 포함되면 NP-완전 문제라고 부르며 NP-완전 문제를 풀 수 있으면 모든 NP 문제를 풀 수 있게 되는 셈이 되기도 하며 풀 수 있는 NP 문제 중 가장 어려운 문제이다. |
문제의 종류
세상에는 다양한 종류의 문제가 존재함
풀 수 있는 문제와 풀 수 없는 문제로 나뉨
풀 수 있는 문제는 해결하는데 필요한 시간에 따라 현실적인 시간에 풀 수 있는 문제와 그렇지 않은 문제로 나뉨
○ 현실적인 시간 안에 풀 수 없는 문제는 근사해를 구하는 것을 목표로 할 수 밖에 없음
○ 문제 푸는데 50년, 150년이 걸리면 풀 수는 있지만 푼다는게 의미가 있을까. 너무 오래 걸림 그래서 몇일내로 풀 수 있는 근사해로 구함
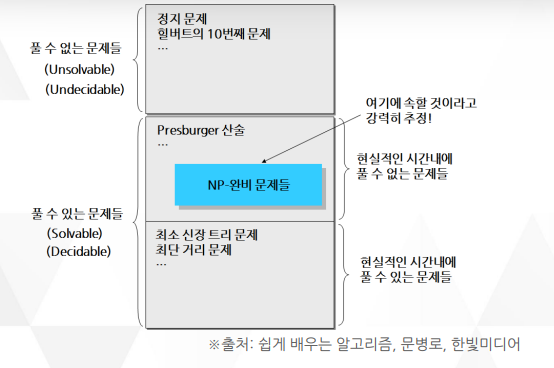
NP 완전 문제
현실적인 시간에 풀 수 없다 추정되면서 서로 강력한 논리적 연관성을 가진 특이한 문제군에 관한 것
현실적인 시간
다항식 시간을 의미 (=현실적인 시간)
문제의 크기가 n이면 그 문제를 푸는데 n의 다항식에 비례하는 시간이 드는 알고리즘
어떤 문제가 다항식 시간에 해결되면 현실적인 시간에 풀 수 있는 경우로 간주

비다항식 시간의 예 (비현실적인 시간)
문제를 해결하는데 비다항식 시간이 소요되면 현실적인 시간에 풀 수 없는 경우로 간주
Yes/No 문제와 최적화 문제
문제는 요구하는 대답의 종류에 따라 나뉜다. (두 문제는 동전의 앞뒷면)
○ Yes 또는 No의 대답을 요구하는 문제 : Yes /NO 문제 (결정 문제)
예) 그래프 G에서 길이가 k 이하인 해밀턴 경로가 존재하는가?
○ 가장 좋은 해를 요구하는 문제 : 최적화 문제
예) 그래프 G에서 길이가 가장 짧은 해밀턴 경로는 얼마인가?
NP 완전군에 속하는 문제들은 현실적인 시간에 풀 수 없다고 강력하게 추정되는 문제
확실하게 100프로 현실적인 시간에 풀 수 없어가 아니라 아마도 풀 수 없을 것이다라고 추정하는 문제가 있다.
아직까지 그 누구도 풀지 않은 문제들도 있다.
지금까지 수없이 많은 NP 완전 문제가 알려졌지만 이들을 다항식 시간에 해결할 수 있는 알고리즘은 발견된 바 없음
많은 액수의 현상금이 걸려있는 문제들이 있다.
P (Polynomial)
다항식 시간에 해결할 수 있는 문제들의 군
결정 문제들 중에서 쉽게 풀리는 것을 모아 놓은 집합
어떤 결정 문제가 주어졌을 때 다항식 시간 이내에 그 문제의 답을 Yes와 No 중의 하나로 계산해낼 수 있는 알고리즘이 존재한다면 그 문제는 P 문제에 해당함
다항식 시간 내에서 더 적은 시간을 소요하는 알고리즘을 개발하는데 초점이 맞추어져 있음
결정론적 튜링 머신으로 다항식 시간 내에 해결이 가능한 문제
컴퓨터 같은 계산장치를 이용해 합리적인 시간 내에 풀 수 있는 형태의 문제
NP (Nondeterministic Polynomial)
NP 문제는 결정 문제들 중에서 적어도 검산은 쉽게 할 수 있는 것으로 모아 놓은 집합
어떤 결정 문제의 답이 YES일 때 그 문제의 답이 YES라는 것을 입증하는 힌트가 주어지면 그 힌트를 사용해서 그 문제의 답이 정말 YES라는 것을 다항식 시간 이내에 확인 할 수 있는 문제
문제의 답이 Yes인 경우 답이 Yes라는 것을 다항식 시간내에 확인할 수 있는 적당한 모범 답안이 존재하는 문제
○ Non-Polynomial의 준말이 아님!
○ 일반적으로 모든 P 문제는 NP문제임
NP-난해 (NP-hard) 문제
적어도 NP 문제 보다는 어려우며 모든 NP 문제를 다항식 시간 내에 어떤 문제로 환원(Reduction) 할 수 있는 경우 그 문제는 NP-난해 문제라고 함
hard란 적어도 어떤 NP 문제보다 해결하기 어렵다는 뜻
NP-난해 문제를 다항식 시간 내에 풀 수 있으면 모든 NP 문제를 다항식 시간 내에 풀 수 있음
○ NP-난해 문제 중 NP 문제가 아닌 것도 있음
○ NP보다 풀기 어려운 문제도 NP-난해 문제일 수 있음
NP-완전 (NP-complete) 문제
NP- 난해 문제에도 포함되며 NP 문제에도 포함되면 NP-완전 문제라고 부름
NP-완전 문제를 풀 수 있으면 모든 NP 문제를 풀 수 있게 되는 셈임
풀 수 있는 NP 문제 중 가장 어려운 문제
○ NP- 완전은 NP-난해의 일부이므로 NP-완전인 문제를 NP-난해라고 불러도 됨
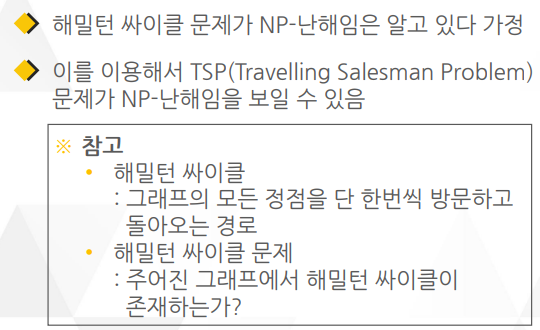
○ 해밀턴 경로 문제도 대표적인 NP-완전 문제들 중 하나

어떤 문제를 다항식 시간 내에 해결할 수 있는가 아닌가는 그 문제를 해결하는데 평균적으로 얼마나 시간이 걸리는가가 아니라 최악의 경우에 시간이 얼마나 걸리는가를 기준으로 함
즉 다항식 시간 내에 해결할 수 없는 경우가 하나라도 있으면 그것은 P 문제가 아니며 P 문제가 아니라고 생각되는 NP 문제라고 하더라도 평균적으로는 다항식 시간 내에 해결할 수도 있음
현재까지의 연구결과
어떤 문제가 NP-완전임이 확인되면 지금까지의 연구 결과로는 이 문제를 현실적인 시간에 풀 수 있는 방법은 아직 없음
그렇지만 이 사실은 아직 증명은 되지 않음
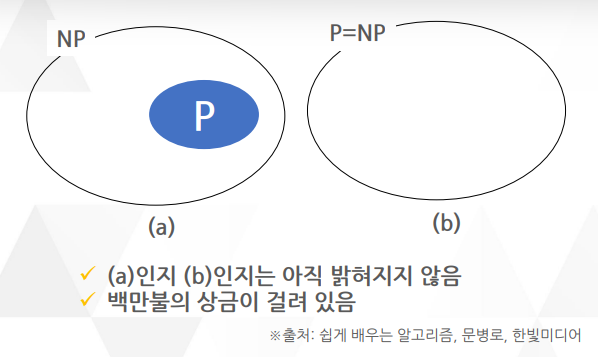
클레이 수학연구소의 21세기 7대 100만 달러가 걸린 밀레니엄 문제 중 하나
복잡도 종류 P와 NP가 같은지에 대한 컴퓨터 과학의 미해결 문제 : 명제 'P=NP'라고 아직 증명되지 않음
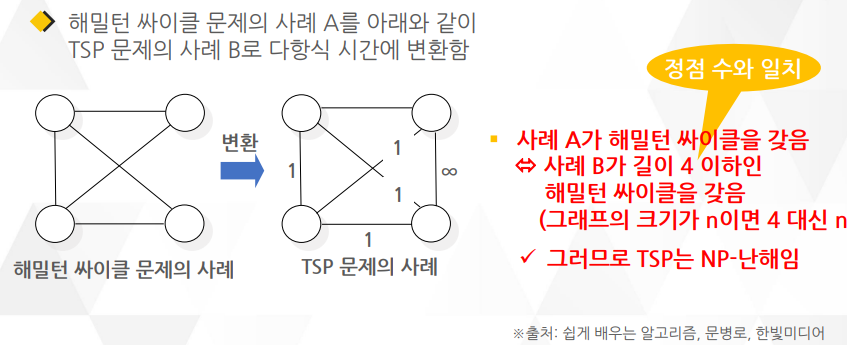
다항식 시간 변환
다른 문제로 바꾸어 풀기 : 다른 문제로 변환한 다음 변환된 문제의 답을 원래 문제의 답으로 삼음




NP 이론의 유용성
어떤 문제가 NP-완전/난해임이 확인되면
○ 쉬운 알고리즘을 찾으려는 헛된 노력은 일단 중지함
○ 주어진 시간 예산 내에서 최대한 좋은 해를 찾는 알고리즘 개발에 집중함