위상 정렬
| 비순환 방향 그래프 | 방향 그래프이면서 사이클이 없는 그래프를 의미하며 여러 공정으로 이루어지는 작업을 모델링하는데 주로 사용한다. |
| 위상 정렬 | 처리해야 할 여러 가지 일들이 있고 이들 사이의 선후 관계가 있으면 이를 유향 그래프로 표현할 수 있는데 이러한 유향 그래프에 각 장점들의 선행 순서를 위배하지 않으면서 모든 정점을 나열하는 것이다. |
| 진입 간선과 진출 간선 | 진입 간선은 유향 그래프에서 한 정점으로 들어오는 간선을 의미하며 진출 간선은 한 정점에서 나가는 간선이다. |
비순향 방향 그래프 (DAG; Directed Acyclic Graph)
방향 그래프이면서 사이클이 없는 그래프
여러 공정으로 이루어지는 작업을 모델링하는데 주로 사용
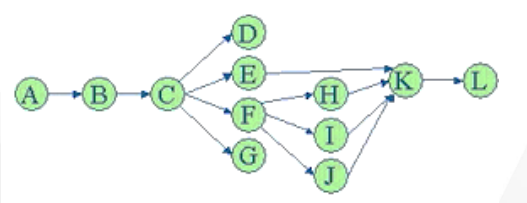
위상 정렬 (Topological Sorting)
처리해야 할 여러가지 일들이 있고 이들 사이의 선후 관계가 있으면 이를 유향 그래프로 표현 가능
해야 할 일들은 정점, 선후 관계는 간선으로 표현
유향 그래프에 존재하는 각 정점들의 선행 순서를 위배하지 않으면서 모든 정점을 나열하는 것
유향 그래프의 정점들을 간선의 방향을 거스르지 않도록 나열하는 것
정렬의 순서는 유향 그래프의 구조에 따라 여러 개의 종류가 나올 수 있음
○ 위상 정렬은 사이클이 있어서는 안됨
○ 사이클이 발생하는 경우 위상 정렬을 수행할 수 없음
일반적인 위상 정렬의 적용은 주로 업무의 일정을 일어나야 할 순서에 따라 배치하기 위하는 것
프로젝트 관리 기법을 평가 및 분석하기 위한 기법(RERT)에 적용하기 위한 목적을 위해 1960년대 초반부터 연구됨
위상 정렬 알고리즘이란 순서가 정해져있는 작업을 차례로 수행해야 할 때 그 순서를 결정해주기 위해 사용하는 알고리즘
위상 정렬은 여러개의 답이 존재할 수 있으며 DAG G(Directed Acyclic Graph)에만 적용이 가능
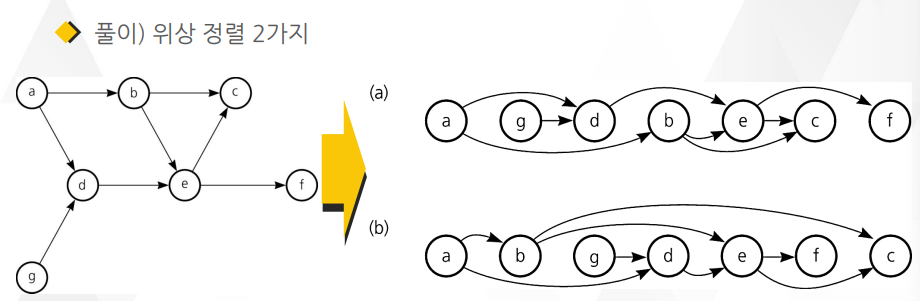
위상 정렬의 예
대학의 선수과목 구조
특정 수상과목에 선수과목이 있다면 그 선수 과목부터 수강해야 하므로 특정 과목들을 수강해야 할 때 위상 정렬을 통해 올바른 수강 순서를 찾아낼 수 있음
일상 생활에서 보통 스케줄 짤 때 많이 쓰는 방법
○ 외출을 하려고 신발을 신기 위해선 먼저 양말 먼저 신어야 함
○ 각 업무를 수행하기 위한 순서를 제공
조건
싸이클이 없는 유향 그래프
위상 정렬
○ 모든 정점을 일렬로 나열하되
○ 정점 x에는 정점 y로 가는 간선이 있으면 x는 반드시 y보다 앞에 위치함
○ 일반적으로 임의의 유향 그래프에 대해 복수의 위상 순서가 존재함
그래프로 확인하기

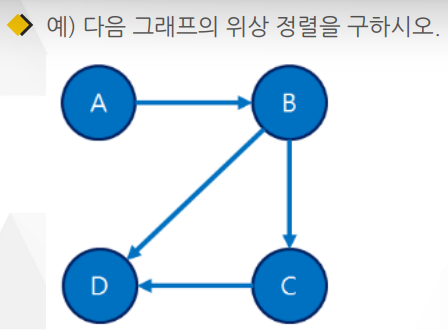

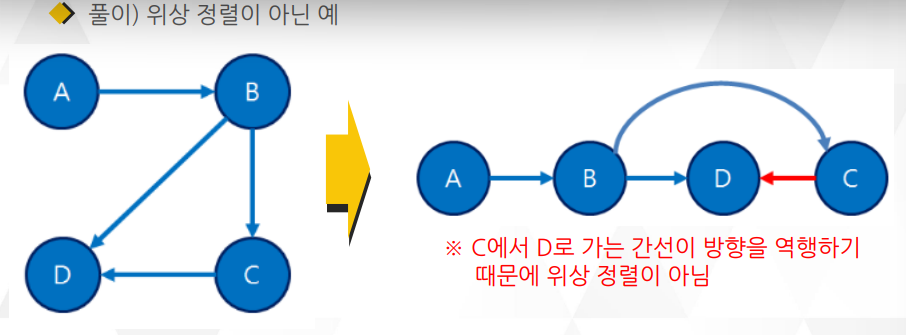
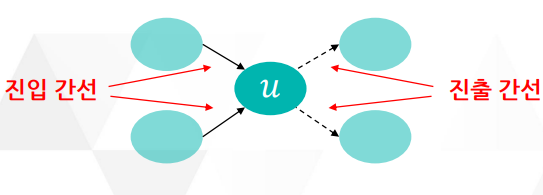
진입 간선 (Incoming Edge)
유향 그래프에서 한 정점을으로 들어오는 간선
진출 간선 (Outgoing Edge)
유향 그래프에서 한 정점에서 나가는 간선
라면 끓이기

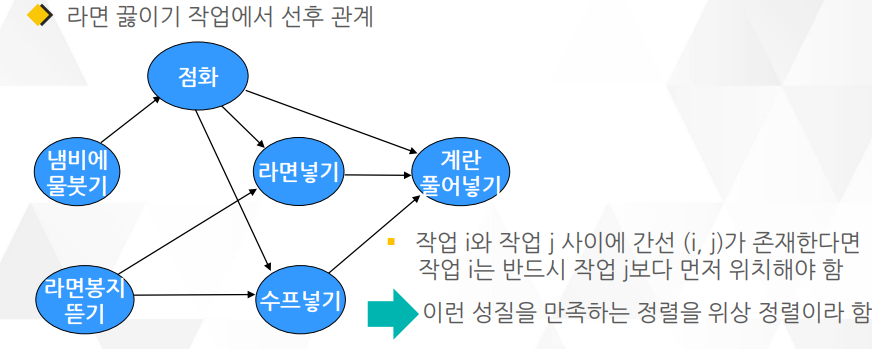
위상 정렬 알고리즘 1 : 라면 끓이기

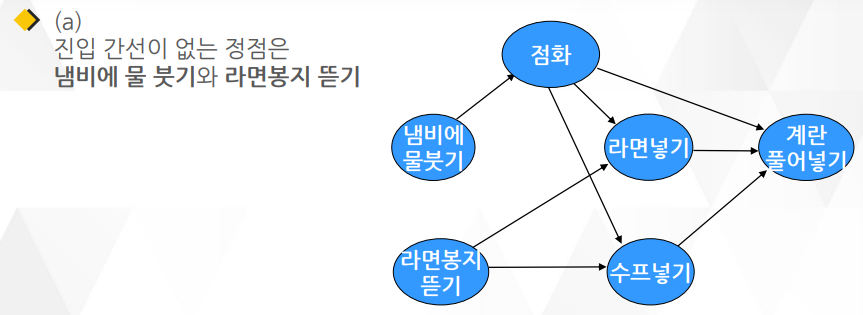
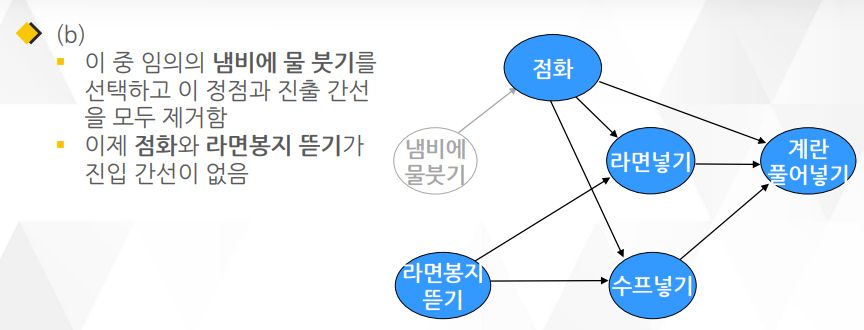
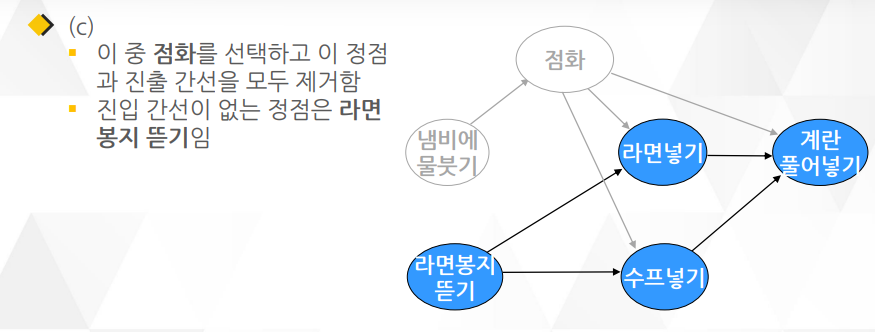
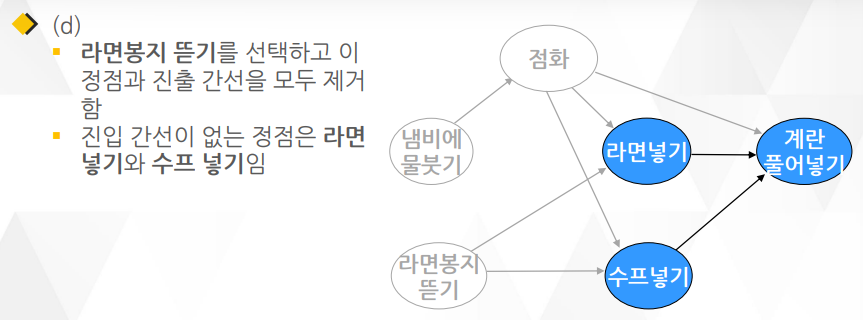
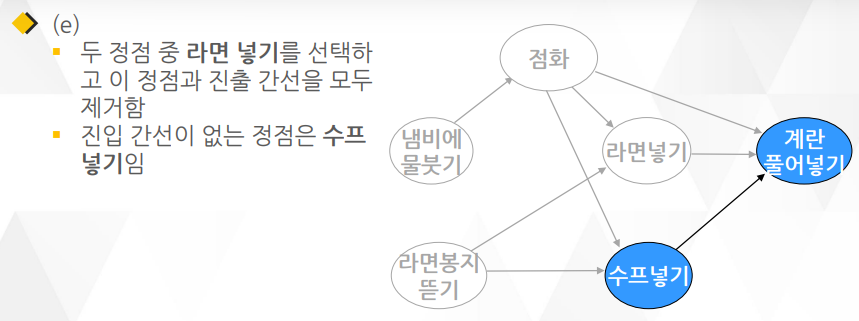


위상 정렬 알고리즘 2 : 라면 끓이기
깊이 우선 탐색(DFS)을 이용한 알고리즘이며 알고리즘1 보다 더 많이 쓰임
○ DFS을 거의 그대로 이용하면서 약간의 요소만 더 추가되어 알고리즘 2가 더 구현하기 간단함
○ DFS와 다른 점은 함수의 맨 끝에 작업이 끝난 정점을 연결 리스트로 관리하는 부분

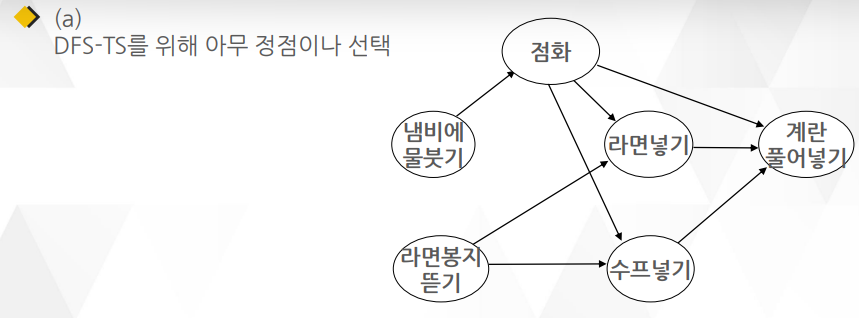
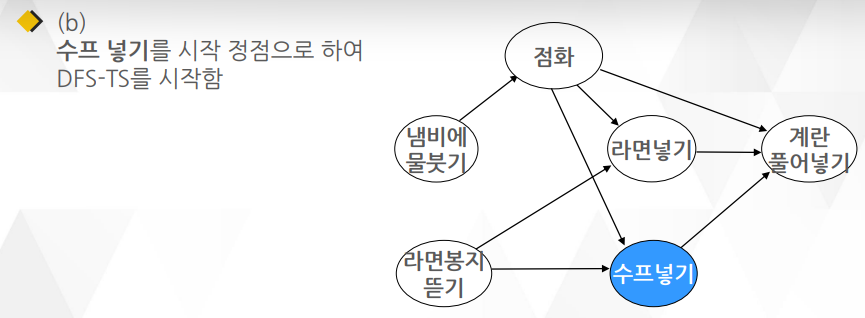
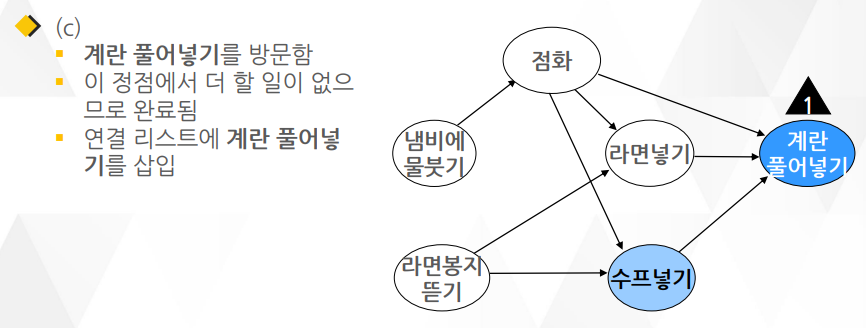
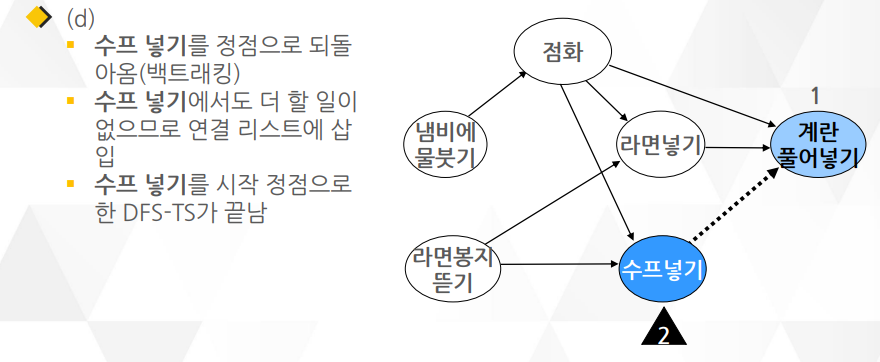
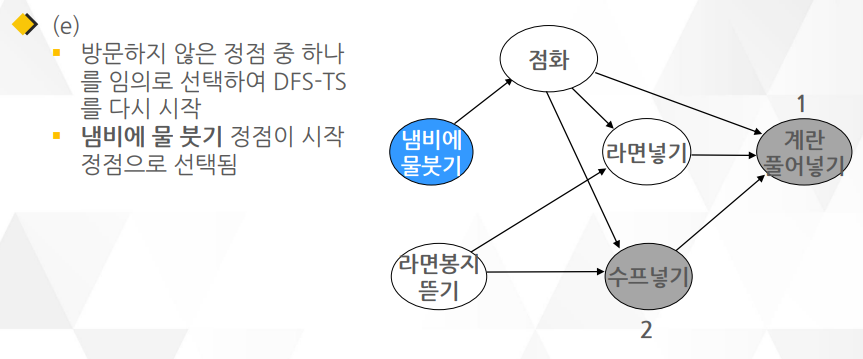
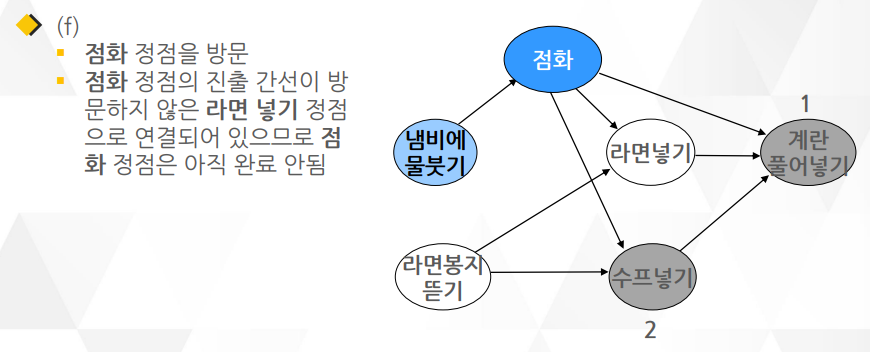

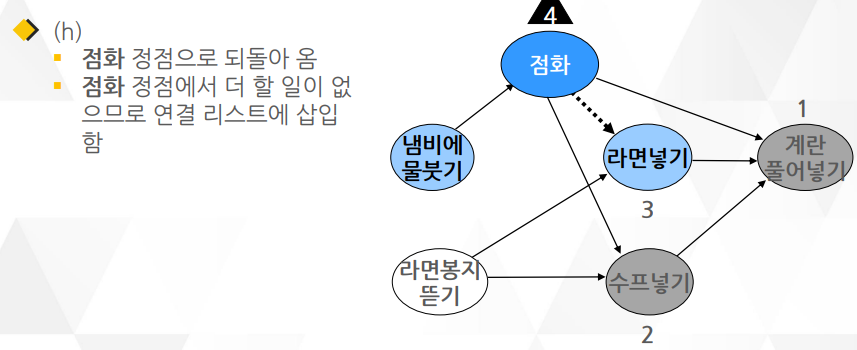
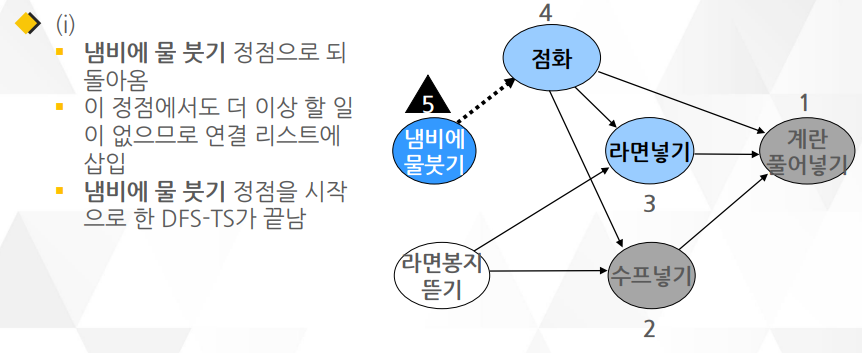
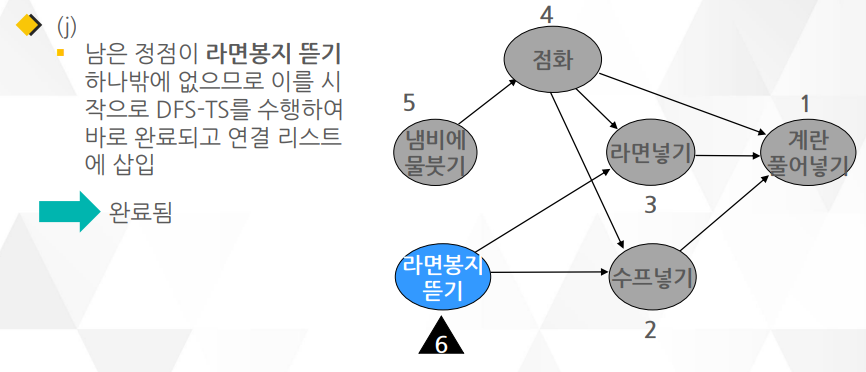
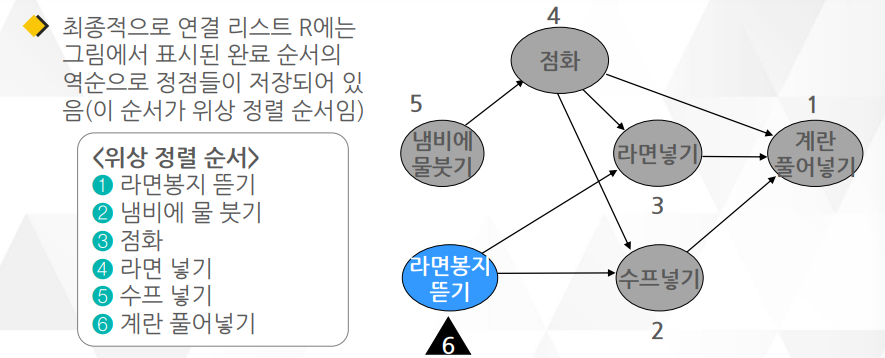
위상 정렬은 숫자들을 크기순으로 정렬하는 것이 아니라 유향 그래프의 정점을 정렬함
위상 정렬이 필요한 경우는 그래프에서 반드시 자신보다 선행되어야 할 일을 다 끝내야만 작업에 들어갈 수 있는(방문할 수 있는) 조건이 주어질 때