그래프의 순회(깊이 우선 탐색, 너비 우선 탐색)와 신장 트리
| 깊이 우선 탐색 | 시작 정점의 한 방향으로 갈 수 있는 경로가 있는 곳까지 깊이 탐색해 가다가 더 이상 갈곳이 없으면, 가장 마지막에 만났던 갈림길 간선이 있는 정점으로 되돌아와 다른 방향의 간선으로 탐색을 계속 반복하여 결국 모든 정점을 방문하는 순회방법이다. 가장 마지막에 만났던 갈림길 간선의 정점으로 가장 먼저 되돌아가서 다시 깊이 우선 탐색을 반복해야 하므로 후입선출 구조의 스택을 사용한다. |
| 너비 우선 탐색 | 시작정점에서 인접한 정점을 모두 차례로 방문하고 나서 방문했던 정점에서부터 다시 인접한 정점을 차례로 방문하는 방식으로 가까운 정점들을 먼저 방문하고 멀리 있는 정점들은 나중에 방문하는 순회방법으로 반복해야 하므로 선입선출인 큐를 사용한다. |
| 신장 트리 | n개의 정점으로 이루어진 무방향 그래프 G에서 n개의 모든 정점과 n-1개의 간선으로 사이클 없는 단순한 연결 그래프로 깊이 우선 탐색을 이용하여 생성된 깊이 우선 신장 트리와 너비 우선 탐색을 이용하여 생성된 너비 우선 신장 트리가 있다. |
그래프 순회 (Graph traversal), 그래프 탐색 (Graph search)
하나의 정점에서 시작하여 그래프에 있는 모든 정점을 한번씩 방문하여 처리하는 연산
그래프 탐색 방법
○ 깊이 우선 탐색 (Depth first search : DFS)
○ 너비 우선 탐색 (Breadth first search : BFS)
그래프 순회의 예 : 우물 파기
한 지점을 골라서 팔 수 있을 때까지 계속해서 깊게 파다가 아무리 땅을 파도 물이 나오지 않으면, 밖으로 나와 다른 지점을 골라서 다시 깊게 땅을 파는 방법
깊이 우선 탐색
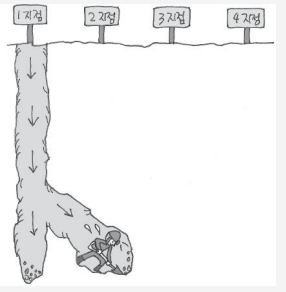
여러 지점을 고르게 파보고 물이 나오지 않으면 파놓은 구덩이들을 다시 좀더 깊게 파는 방법
너비 우선 탐색
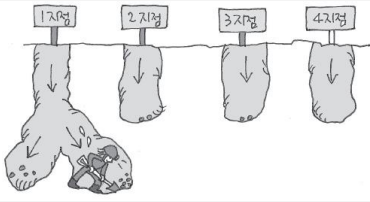
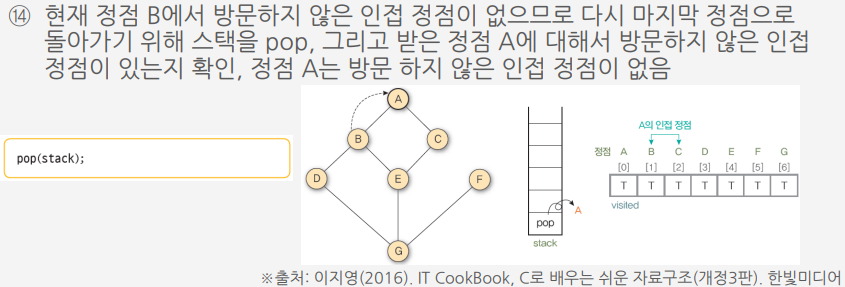
깊이 우선 탐색
순회 방법
○ 시작 정점의 한 방향으로 갈 수 있는 경로가 있는 곳까지 깊이 탐색해 가다가 더 이상 갈 곳이 없으면, 가장 마지막에 만났던 갈림길 간선이 있는 정점으로 되돌아와 다른 방향의 간선으로 탐색을 계속 반복하여 결국 모든 정점을 방문하는 순회방법
○ 가장 마지막에 만났던 갈림길 간선의 정점으로 가장 먼저 되돌아가서 다시 깊이 우선 탐색을 반복해야 하므로 후입선출 구조의 스택 사용

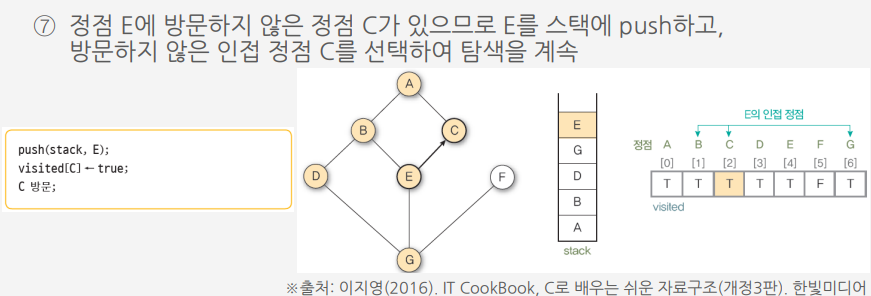
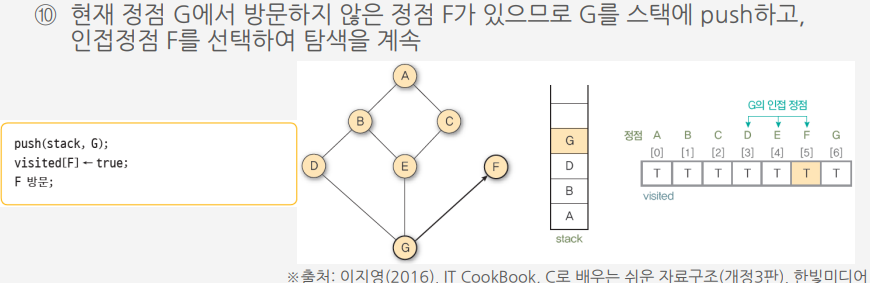
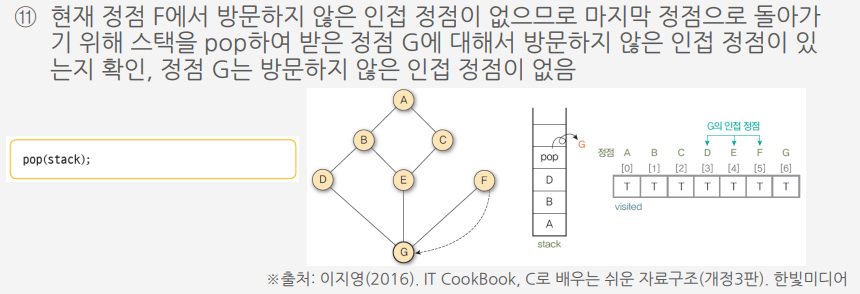
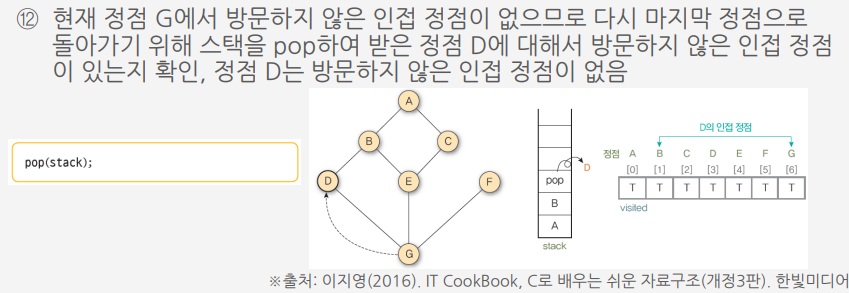
알고리즘에 따라 그래프 G9를 깊이 우선 탐색하는 과정

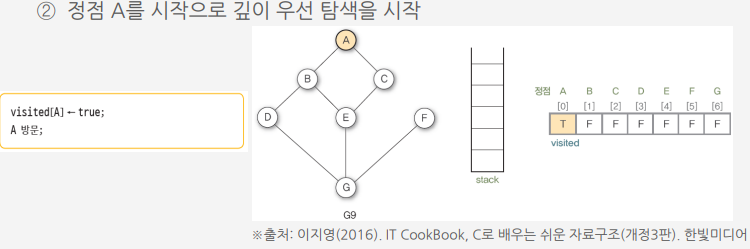

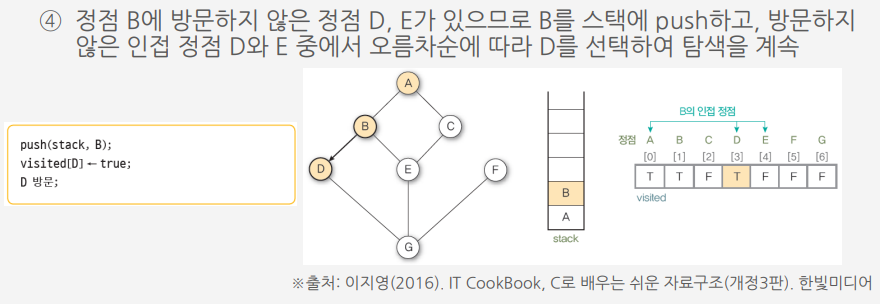







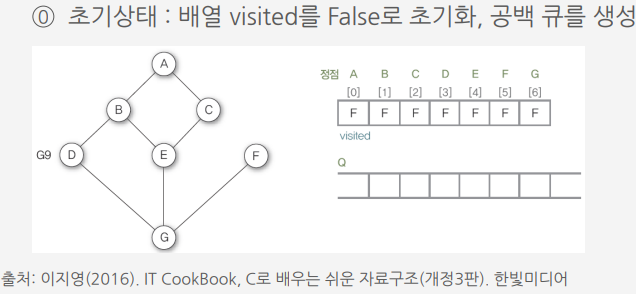
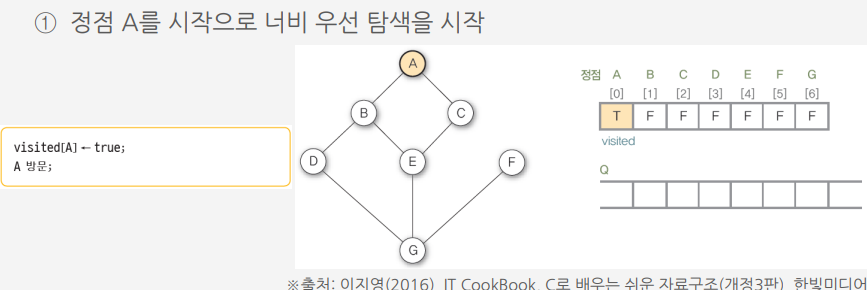
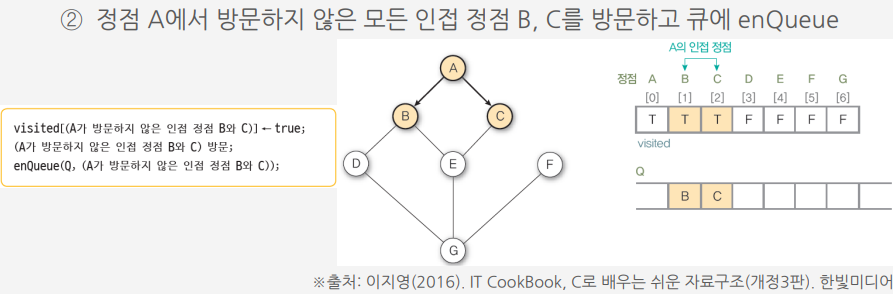
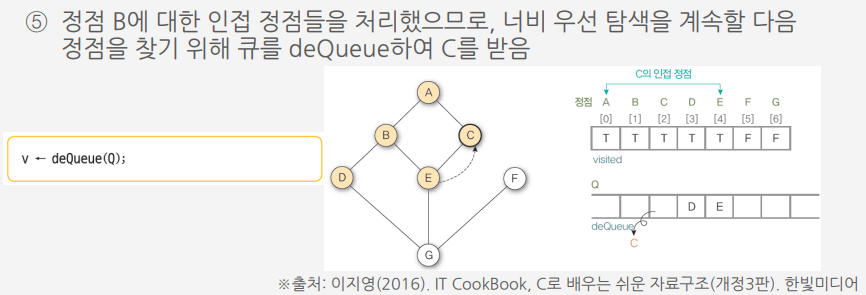
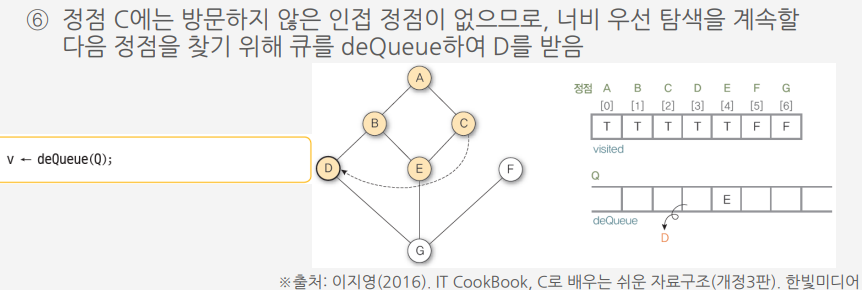
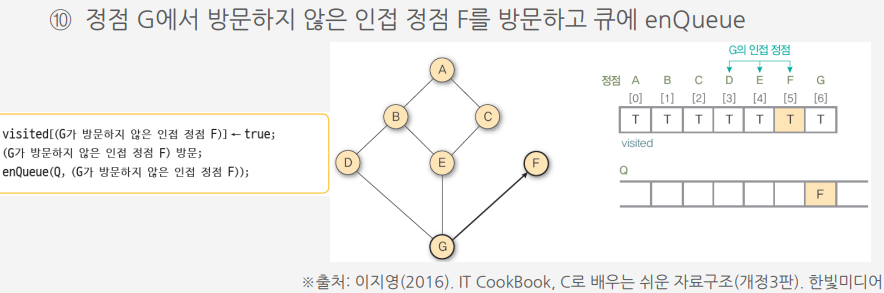
너비 우선 탐색 (Breadth first search : BFS)
시작정점에서 인접한 정점을 모두 차례로 방문하고 나서 방문했던 정점에서부터 다시 인접한 정점을 차례로 방문하는 방식
○ 가까운 정점들을 먼저 방문하고 멀리 있는 정점들은 나중에 방문하는 순회방법
○ 큐를 사용

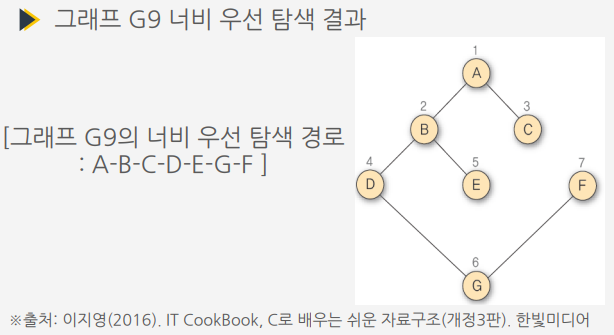
알고리즘에 따른 그래프 G9의 너비 우선 탐색 과정







신장 트리 (Spanning tree)
n개의 정점으로 이루어진 무방향 그래프 G에서 n개의 모든 정점과 n-1개의 간선으로 사이클 없는 단순한 연결 그래프

● 깊이 우선 신장 트리(Depth first spanning tree)
깊이 우선 탐색을 이용하여 생성된 신장 트리
● 너비 우선 신장 트리 (Breadth first spanning tree)
너비 우선 탐색을 이용하여 생성된 신장 트리

최소 비용 신장 트리 (Minimum cost spanning tree)
무방향 가중치 그래프에서 신장 트리를 구성하는 간선들의 가중치 합이 최소인 신장 트리
가중치 : 그래프의 간선에 주어진 가중치비용이나 거리, 시간을 의미하는 값
최소 비용 신장 트리를 만드는 알고리즘
○ 크루스칼(Kruskal)의 알고리즘
○ 프림(Prime)의 알고리즘
크루스칼 알고리즘 |
가중치가 높은 간선을 제거하면서 최소 비용 신장 트리를 만드는 방법

크루스칼 알고리즘Ⅰ을 이용하여 G10의 최소 비용 신장 트리 만들기

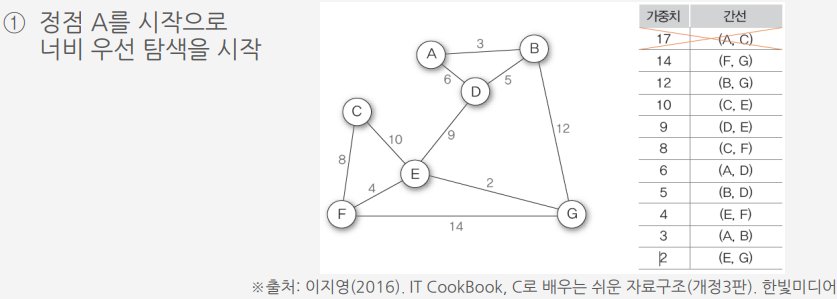

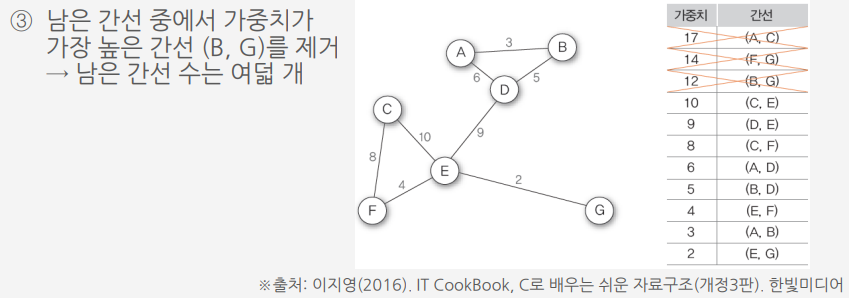

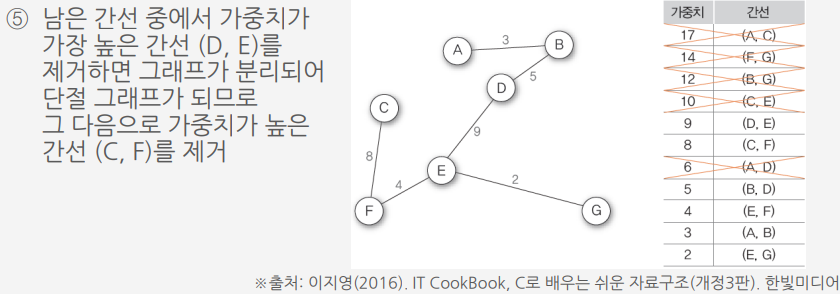


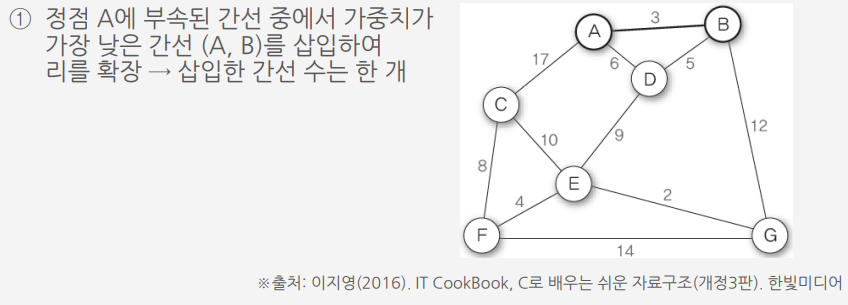
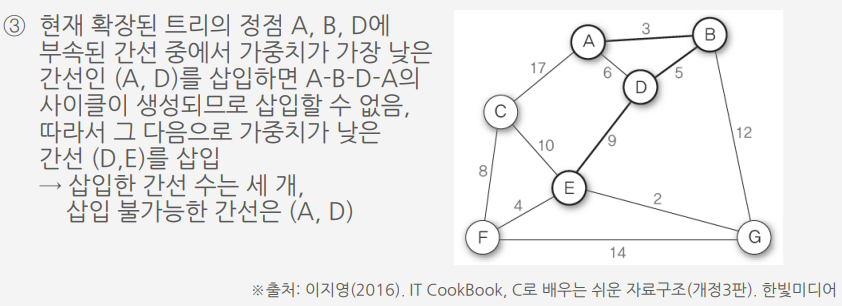
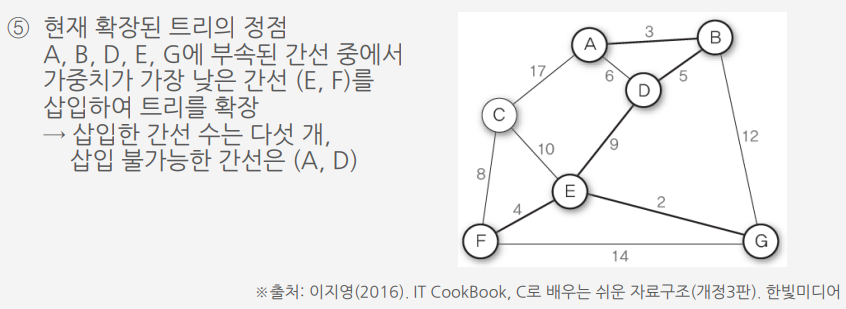
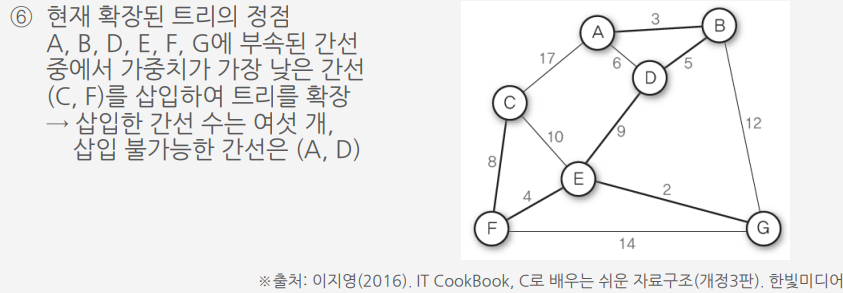
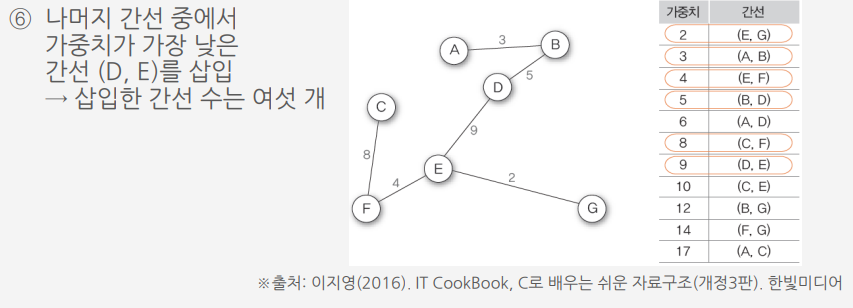
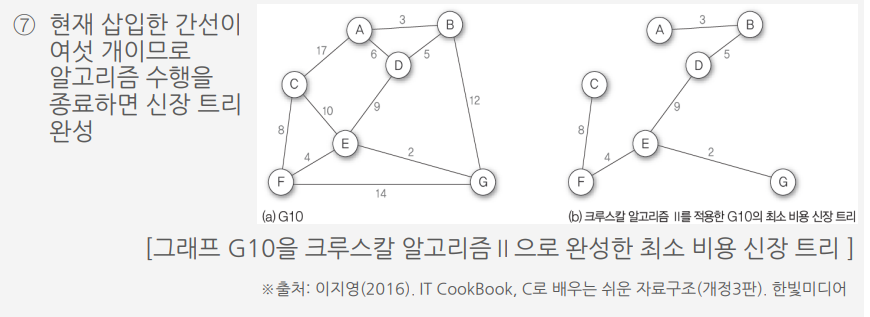
크루스칼 알고리즘 ||
가중치가 낮은 간선을 삽입하면서 최소 비용 신장 트리를 만드는 방법

크루스칼 알고리즘Ⅱ를 이용하여 G10의 최소 비용 신장 트리 만들기
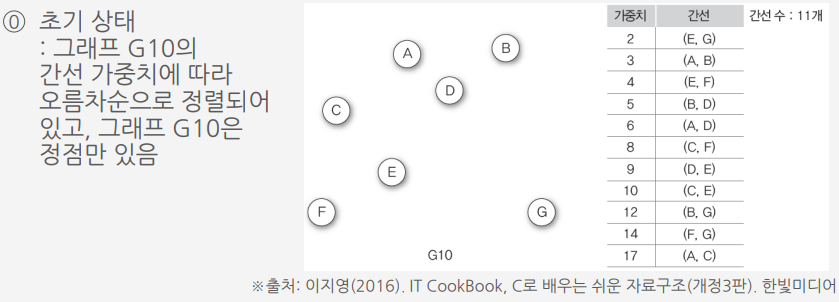





프림 알고리즘
간선을 정렬하지 않고 하나의 정점에서 시작하여 트리를 확장해 나가는 방법

프림 알고리즘을 이용하여 그래프 G10의 최소 비용 신장 트리 만들기