오일러 사이클과 해밀턴 사이클
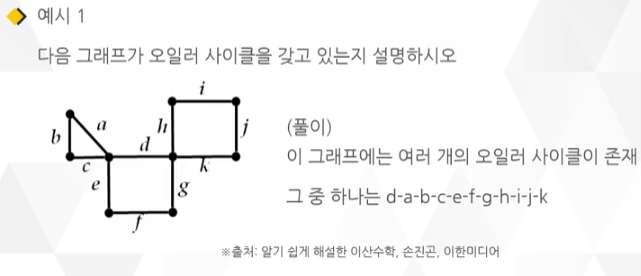
| 오일러 사이클 | 그래프에서 각 간선을 정확하게 한 번씩만 경유해서 그래프의 모든 간선을 지날 수 있는 경로를 오일러 경로라고 하고 오일러 경로가 존재하고 출발 정점과 최종 도착 정점이 같으면 오일러 사이클이라고 한다. |
| 해밀턴 사이클 | 그래프에서 모든 정점을 포함하는 사이클이 있을 때 이 사이클을 주어진 그래프의 해밀턴 사이클이라고 한다. |
| 트리 | 사이클이 없는 연결 그래프를 트리라 하며 운영체제의 파일 시스템, 검색 엔진, 데이터베이스, 컴파일러 등 다양한 분야에서 활용된다. |
그래프의 이론
유한개의 정점과 간선의 결합 방법에 대한 이론
어떤 그래프에서 정점을 도시라 하고 간선을 도로로 간주한다면 경로는 어떤 도시를 출발하여 몇몇 도시를 거쳐 어떤 도시에서 끝내는 여행에 해당함
예 ) 택배 기사가 택배 배달해야 할 때 배달 지역은 어떤 규칙성이 없어 여러 지역이 분포됨
어떤 규칙성 없이 필요할 때마다 연결하여 사용하는 비선형 자료구조가 그래프임
그래프 응용
그래프 이론은 회사의 조직도나 가계도, 토너먼트의 조합, 전기회로의 배선도, 집적회로 등 전기 회로망 문제, 통신망, 물자의 수송로 등에 응용
철도망과 도로망에서 역과 역이 몇 개의 선으로 연결되어 있는지, 바꾸어 타는 것은 어느 역에서 하면 좋은지 등을 결정하는데 활용
Chinese Postman Problem
우체부가 모든 거리의 집에 편지를 전하고 우체국으로 돌아오려할 때 최저 거리의 길을 찾는 문제
시작점에서 모든 노드를 다 거쳐서 다시 시작점을 돌아오는 그래프
도시의 눈치우기
제설기 1대가 모든 도로의 눈 치우기 위해 필요한 방법
그래프 시초
그래프 이론은 스위스의 수학자 오일러가 연구한 쾨니히스베르크의 다리 건너기 문제가 그 시초
그 후 영국의 수학자 해밀턴에 의하여 정십이면체의 각 정점을 세계의 도시로 보고, 각 변은 그 사이를 오가는 여행로로 보았을 경우, 이 여행로를 따라서 각 도시를 단 한 번만 지나가는 여행 코스를 찾아내라는 '해밀턴의 문제'가 제시됨

해밀턴 사이클은 1857년에 만들어진 아이코시안(Icosian) 퀴즈 문제에서 비롯됨
이 퀴즈 문제는 12면체 20개의 각 정점에 도시 이름을 적고 어느 한 도시에서 출발하여 모서리를 따라서 다른 모든 19개의 도시를 방문하고 처음 출발했던 도시로 돌아오는 게임
물론 각 도시는 단 한번만 방문할 수 있음
오일러 사이클 (Euler Cycle)

쾨니히스베르크 다리 문제는 7개의 다리를 한 붓 그리기로 다 건너는 문제임
2개의 섬과 7개의 다리로 구성된 공원에서 7개의 다리를 모두 지나가는데 이미 지나갔던 다리는 다시 거치지 않고 갈 수 있는 전체 경로를 해결하는데 오일러는 그래프 이론을 사용하였음

오일러는 이 문제를 해결하는데 각 정점에 연결된 간선의 개수가 모두 짝수일 때 가능함을 증명함
각 간선을 정확하게 한번씩만 경유해서 그래프의 모든 간선을 지날 수 있는 경로가 존재하고 출발 정점과 최종 도착 정점이 같으면 오일러 사이클이라고 함
한 붓 그리기 문제
붓을 한 번도 종이 위에서 떼지 않고 같은 곳을 두 번 지나지 않으면서 어떤 도형을 그릴 수 있느냐 하는 문제
○ 그래프의 모든 정점의 차수가 짝수만으로 되어 있을 때 가능
○ 또는 홀수 차수인 정점이 2개인 그래프도 그 한쪽을 출발점, 나머지 하나를 도착점으로 하는 경우에는 한 붓 그리기가 가능함
오일러 경로 (Euler Path)
그래프에서 간 간선을 정확하게 한 번씩만 경유해서 그래프의 모든 간선을 지날 수 있는 경로가 존재한다면 그래프는 오일러 경로를 갖는다고 한다.
임의의 두 정점 사이의 경로(Path)는 두 정점을 연결하는 간선들을 나열한 것이며 경로에서 같은 간선은 두 번 이상 지나갈 수 없음
오일러 경로, 오일러 사이클에서는 정점에 상관없이 모든 간선을 반드시 한 번씩 지나야 함
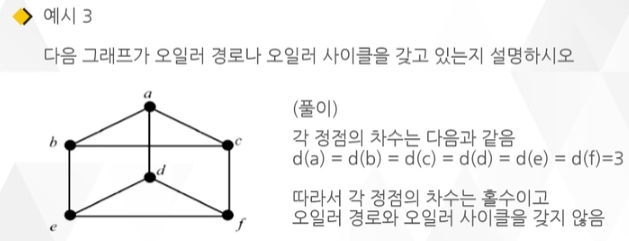
그래프 G가 오일러 경로를 갖기 위한 필요충분조건은 그래프 G가 연결 그래프이고 홀수 차수의 정점이 2개인 것임

그래프가 오일러 사이클을 가진다면 모든 정점의 차수는 짝수임
그래프가 연결 그래프이고 모든 정점의 차수가 짝수라면 그래프는 오일러 사이클을 가짐

해밀턴 사이클 (Hamiltion Path)
그래프 G=(V,E)가 주어진 모든 정점들을 정확하게 한 번만 경유하는 경로가 있는 그래프를 해밀턴 경로가 존재한다고 함
○ 그래프에서 모든 정점을 정확히 한번만 지나는 경로
○ 어떤 두 정점에 인접하는 간선이 존재하지 않더라도 다른 정점들과 간선들을 통해 두 정점이 연결되면 두 정점 간의 경로가 존재하는 것임
그래프의 한 정점에서 출발하여 인접한 간선과 이웃하는 정점을 따라 교대로 통과하되 시작점을 제외한 모든 정점을 단 한 번씩만 지나서 시작점으로 되돌아오는 것을 해밀턴 사이클이라 함
시작점과 끝점이 같은 해밀턴 경로
연결된 그래프가 각 정점을 정확히 한 번만 경유하는 경로인 사이클
○ 정점을 한 번씩만 지나고 다시 출발 정점으로 돌아오는 사이클
○ 해밀턴 사이클이 존재한다는 것은 해밀턴 경로가 존재한다는 것이지만 그 역은 성립하지 않음
○ 해밀턴 사이클을 갖는 모든 그래프
오일러 사이클은 그래프의 간선에 대한 탐색 방법이였다면
해밀턴 사이클은 그래프의 정점에 대한 탐색 방법임
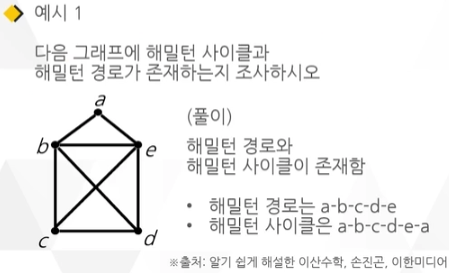
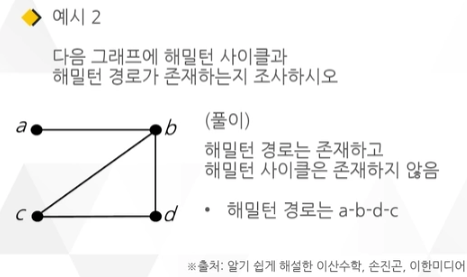
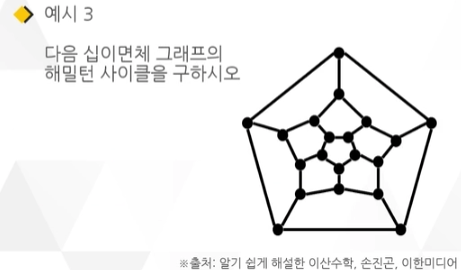



해밀턴 그래프
주어진 그래프에서 원하는 경로나 사이클 등을 찾는 방법은 그래프 이론에서 매우 중요한 문제임
모든 도시를 방문해야 하는 판매원의 경우 각 도시를 한 번씩만 거칠 때 가장 경제적임
즉, 방문할 도시들은 정점으로 표현할 수 있으며 각 도시를 정확히 한 번만 경유하는 최적의 방문 경로를 찾는 데 목적이 있음
방문 판매원 문제 (Traveling Salesman Problem)
해밀턴 사이클은 일상생활의 문제를 해결할 때에도 적용할 수 있는데 이러한 대표적인 예로 방문 판매원 문제가 있다.

문제
어떤 방문 판매원이 수많은 도시들을 순회하여 출발한 도시로 되돌아와야 하는데 이때 각 도시를 단 한번만 방문하되 총 이동 거리를 가능한 짧게 하고자 한다. 각 도시들 사이의 거리가 다양하게 주어져 있을 때(가중치가 주어져 있을때), 방문 판매원은 어떤 경로를 선택해야 할까?
풀이
주어진 도시들을 정점으로, 두 도시를 잇는 도로를 간선으로, 도시 간 거리를 변의 가중치로 하여 완전 가중치 그래프를 만들면 이 문제는 주어진 가중치 그래프에서 모든 정점을 통과하면서 총 가중치가 최소인 사이클을 찾는 것이 됨
즉, 최소 가중치 해밀턴 사이클을 찾는 문제가 됨
방문 판매원 문제는 겉보기에는 무척 간단해 보이지만
정점이 늘어나면 기하급수적으로 어려워져서 조합적 최적화 분야에서 악명 높은 NP-난해 문제(NP-hard Problem)로서 문제를 푸는 효율적인 알고리즘이 아직 알려져 있지 않음
트리 (Tree)

사이클이 없는 연결 그래프를 트리라 함
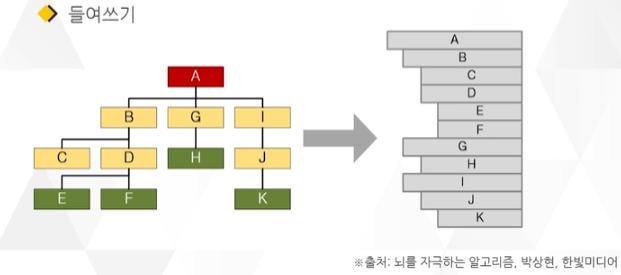
○ 상위 원소에서 하위 원소로 내려가면서 확장되는 트리(나무)모양의 구조
○ 운영체제의 파일 시스템, 검색 엔진, 데이터베이스, 컴파일러 등 다양한 분야에서 활용되는 자료 구조
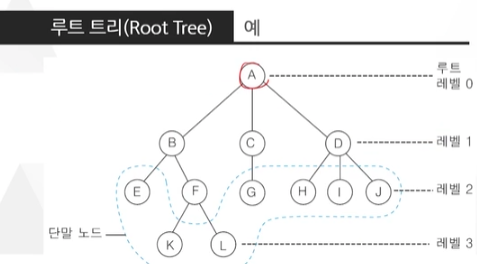
루트 트리 (Root Tree)
루트 트리 T는 다음 조건을 만족하는 1개 이상의 노드 (v1, v2, ... vn)들의 유한집합