다차원 배열(2차원, 3차원)과 행렬(정방,전치,희소)
다차원 배열과 희소행렬
| 2차원 배열 | ● 2차원 배열을 이용한 선형리스트 구현으로는 데이터를 표현하는데 순서 기준이 두 종류 있는 경우와 행 인덱스와 열 인덱스가 있는 2차원 배열을 사용한다. ● 2차원 배열구조를 논리적으로 표현할 때는 행과 열의 구조로 나타내지만 실제로 메모리에 저장될 때는 1차원 구조로 저장된다. |
| 3차원 배열 | ● 3차원 배열을 이용한 선형리스트 구현으로는 데이터를 표현하는데 순서 기분이 세 정류 있는 경우와 면 인덱스, 행 인덱스, 열 인덱스가 있는 3차원 배열을 사용한다. ● 논리적으로 표현할 때는 면과 행, 열의 구조로 나타내지만 실제로 메모리에 저장될 때는 1차원 구조로 저장된다. |
| 행렬 | ● 행렬은 행과 열로 구성된 자료구조이다. ● m * n 행렬은 행 개수가 m개, 열 개수가 n개인 행렬이다. ● 정방행렬은 행렬 중에서 m과 n이 같은 행렬이다. ● 전치행렬은 행렬의 행과 열을 서로 바꿔 구성한 행렬이다. ● 희소행렬은 행렬의 원소 중에서 많은 항들이 0으로 구성된 행렬이다. |
01. 2차원 배열을 이용한 선형리스트 구현
1. 2차원 배열을 이용한 선형 리스트 구현
(1) 2차원 배열을 이용한 구현
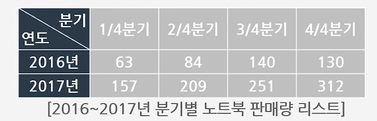
분기와 연도를 모두 표현해야 하므로 순서가 두 종류가 필요하다.
따라서 행 인덱스와 열 인덱스가 있는 2차원 배열을 사용한다.
2차원 배열구조를 논리적으로 표현할 때는
행과 열의 구조로 나타내지만 실제로 메모리에 저장될 때는 1차원 구조로 저장된다.
왜 1차원 구조로 저장될까?
메모리는 1차원 배열형태로 구성되어 있기 때문이다.
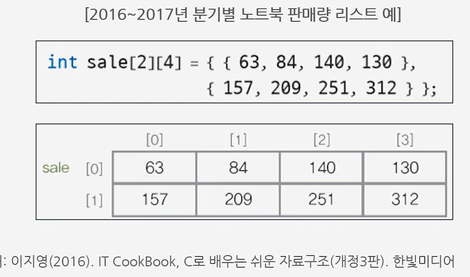
int sale[2][4]
● 행은 년도값, 열은 분기값을 가지는 정수형 배열을 만들었다.
● 행의 번호 0번, 1번
● 열의 번호 0번, 1번, 2번, 3번
{{ 63, 84, 140, 130},
{157, 209, 251, 312}};
첫 번째 줄에는 1분기, 2분기, 3분기, 4분기의 값
두 번째 줄에도 1분기, 2분기, 3분기, 4분기의 값을 초기화하였다.
2. 2차원 배열의 물리적 저장 방법
2차원 배열의 물리적인 저장 방법은 뭘까?
2차원의 논리적 순서를 1차원의 물리적 순서로 변환하는 방법을 사용하여 저장한다.
(1) 행 우선 순서 방법 (Row Major Order)
행을 우선으로 먼저 1행 저장하고, 2행을 저장한다.
2차원 배열의 첫 번째 인덱스인 행 번호를 기준으로 사용하는 방법
sale[0][0]=63
sale[0][1]=84
sale[0][2]=140
sale[0][3]=130
sale[1][0]=157
sale[1][1]=209
sale[1][2]=251
sale[1][3]=312
(2) 열 우선 순서 방법 (Column Major Order)
열을 우선으로 먼저 0행 0열, 1행 0열, ...으로 저장된다.
2차원 배열의 마지막 인덱스인 열 번호를 기준으로 사용하는 방법
sale[0][0]=63
sale[1][0]=157
sale[0][1]=84
sale[1][1]=209
sale[0][2]=140
sale[1][2]=251
sale[0][3]=130
sale[1][3]=312
A배열의 임의의 i, j 원소 위치를 계산하는 방법

행의 개수가 엔i이고 열의 개수가 엔j일때
[i][j] 이렇게 가지고 있는것이다.
행우선이든 열우선이든 메모리에 1차원으로 쭉 저장이된다.
시작 주소는 임의의 주소 알파
| 행 우선 |
임의의 주소는 모르니깐 알파주소에서 i번째 행 * 몇개의 컬럼(열)인지 컬럼의 개수를 곱하고 j 지금 현재 열의 위치, 몇번째 열인지를 더해주면 행의 번호를 구할 수 있다. 그리고나서 l은 메모리의 크기를 나타낸다. int이라면 4바이트씩, double이면 8바이트씩 연속해서 할당이 되어진다. 이것을 곱해준다. 즉, 행우선이면 행번호에서 열의 개수를 곱하고, j 위치를 더해서 메모리 크기를 곱하면 된다. |
| 열 우선 |
열 우선일때에는 열과 몇개의 컬럼인지를 먼저 곱하고 행을 더한다 행 우선은 행먼저 계산하고 열 우선은 열먼저 계산한다. 즉, 열 우선은 열 우선이기때문에 열에다가 지금 행이 몇개 있는지를 곱한 다음에 행 몇번째에 있는지 i첨자를 더하고 실제 메모리 크기를 곱해준다. |
3. 2차원 논리 순서를 1차원 물리 순서로 변환


sale[2][4] 2행 4열의 sale 정수 배열에 대해서
2차원 논리 순서를 1차원 물리 순서로 변환하는 것을 그림으로 나타낸것이다.
예 )

행 우선은
행 번호에다가 열의 개수를 곱한 다음에 실제 열의 첨자를 더해서 메모리의 크기를 곱하면 된다.
열 우선은
열 번호에 행의 개수를 곱한 다음에 지금 현재 행의 번호를 더해서 메모리의 크기를 곱하면 된다.
예제 ) 배열이 int a[4]10로 선언되어있다.
4행 10열이다.
시작 주소는 1000이고 행우선으로 a[2][8]의 위치는
1000+(2 * 10 + 8)*4 = 1112번지에 저장되어 있다.
시작 주소는 1000이고 열우선으로 a[2][8]의 위치는
1000+(8 * 4 + 2)*4 = 1136번지에 저장되어 있다.
4. 2차원 배열의 논리적.물리적 순서 확인하기 프로그램

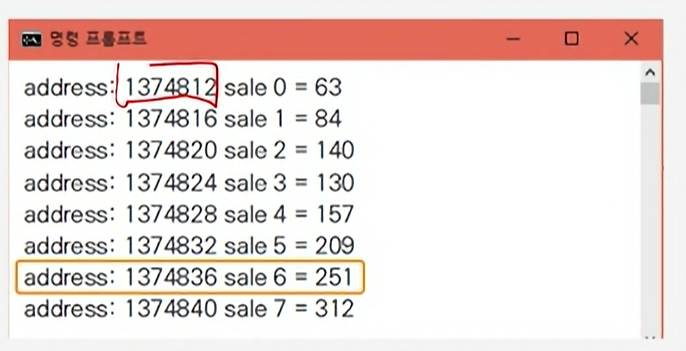

02. 3차원 배열을 이용한 선형리스트 구현
1. 3차원 배열을 이용한 선형 리스트 구현
3차원 배열을 이용한 구현
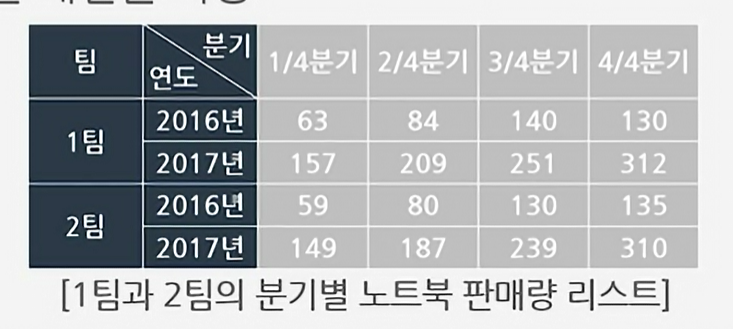

연도와 분기 그리고 팀 순서도 나타내야 하므로
세 종료 순서를 표현해야 한다.
이럴 때는
면 인덱스, 행 인덱스, 열 인덱스가 있는 3차원 배열을 사용한다.
3차원 배열은 대괄호를 3개 사용한다.
면우선이다. 공책 한 페이지를 다 작성하면 그 다음 페이지로 넘어간다. 그 페이지 하나를 면이라고 한다.
그 면 공책 한페이지에 행우선으로 차례대로 채워진다. 이런구조로 3차원배열을 처리한다.
2. 3차원 배열의 물리적 저장 방법
3차원 배열의 물리적 저장 방법은
3차원의 논리적 순서를 1차원의 물리적 순서로 변환하는 방법을 사용해 저장해야 된다.
A[i][j][k]의 위치(순서) 계산 방법

| 면 우선 |
3차원 배열의 첫 번째 인덱스인 면 번호를 기준으로 사용하는 방법 i가 면이다. j가 행이고 k가 열이다. 몇번째 공책의 몇칸 몇줄인지를 알아야 된다. 면이 꽉 채워지면 그 다음면에서 몇줄 몇칸인지를 알아봐서 그 줄에 몇번째 칸인지를 찾게 되어지는 형태로 구성된것이다. 임의의 주소 알파부터 시작해서 몇번째 면에 행갯수와 열갯수를 곱해주게되면 면의 위치를 찾은것이다. 그 다음 면에서의 행에다가 열의 개수를 곱하면 된다. 그리고 열의 위치를 더한다. 위의 가로친것들의 값도 다 더한다음에 실제 메모리의 주소를 곱한다. |
| 열 우선 |
3차원 배열의 마지막 인덱스인 열 번호를 기준으로 사용하는 방법 면,행,열에서 열 기준으로 한다는것이다. 알파주소로부터 시작하여 열에 면과 행을 곱하면 된다. 행에다가 면을 곱한다. 면을 더한다음에 실제 메모리 크기만큼 곱한다. |
3. 3차원 논리 순서를 1차원 물리 순서로 변환

주로 C언어 컴파일러에서 물리적인 순서로 변환하는 방법으로는
3차원 배열에서는 면우선,
2차원 배열에서는 행우선으로 변환해서 사용되어진다.
4. 3차원 배열의 논리적.물리적 순서 확인하기 프로그램
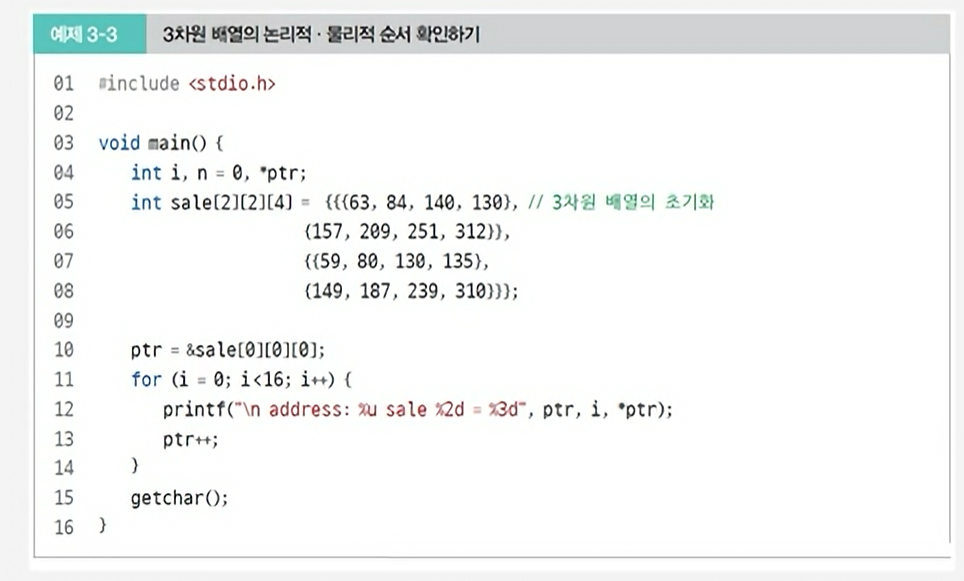


03. 희소 행렬의 순차 자료구조 구현
1. 행렬의 선형 리스트 표현
행렬(Matrix)의 개념
행과 열로 구성된 자료구조의 종류
| m*n 행렬 | 행 개수가 m개, 열 개수가 n개인 행렬 |
| 정방행렬 | 행렬 중에서 m과 n이 같은 행렬 |
| 전치행렬 | 행렬의 행과 열을 서로 바꿔 구성한 행렬 3행 2열의 행렬을 → 2행 3열로 바꾸는것이다. |
행렬과 전치행렬 표현과 예
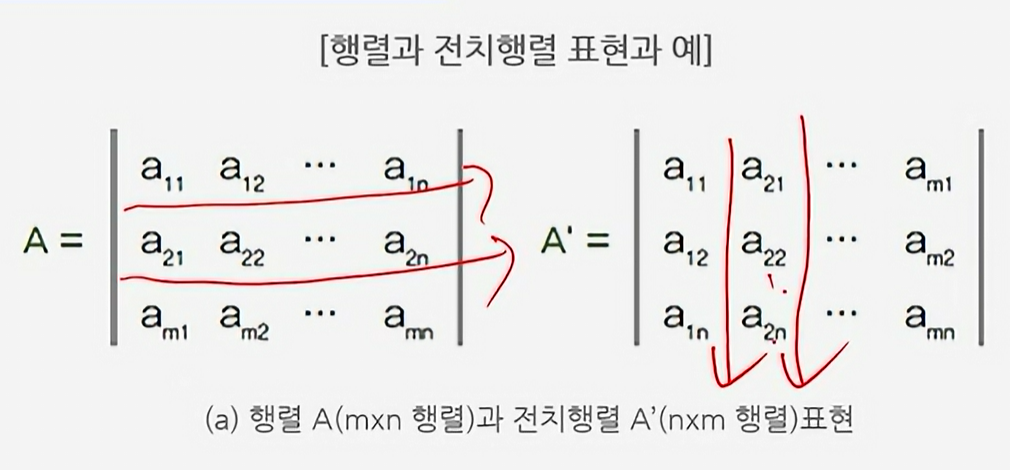
전치행렬을 그림으로 나타낸것이다.
● 행과 열의 위치를 바꾼것이다.
● 행 a11, a12...을 열 a11, a12,...로 바꾸었다.

A[3][4] → A[4][3]
3행 4열의 형태이다. 이것을 4행 3열로 바꾸었다. 이것을 전치행렬이라고 한다.
행렬과 A의 2차원 배열 표현 예
행렬의 각 원소는 행과 열로 표현할 수 있으므로
선형 리스트 표현 m*n 행렬 A를 아래와 같이 2차원 배열 A[m][n]으로 표현할 수 있다.

실제 수학에서는 행렬을 왼쪽처럼 표현한다.
절대치 값처럼 표현해서 행과 열을 표현한다.
컴퓨터안에서 논리적 표현을 하는 C언어는 오른쪽처럼 표현한다.
테이블형태로 값을 논리적으로 표현한다. 가로는 행, 세로는 열, 배열의 시작번호는 0을 갖는 구조로 표현된다.
2. 희소행렬(Sparse Matrix)
행렬의 원소 중에서 많은 항들이 0으로 구성된 행렬
원소 대부분이 0이라 실제로 사용하지 않는 공간이 많아 기억 공간의 활용도가 떨어진다.
따라서 기억공간을 좀더 효율적으로 사용하려면
0이 아닌 값이 있는 원소만 따로 배열로 구성하는 방법을 사용할 수 있다.
희소행렬 B의 2차원 배열 표현 예1

왼쪽 그림을 보면 0값이 많다.
0이 아닌 숫자값들은 몇개 없다. 이런 행렬을 희소행렬이라고 한다.
이것을 컴퓨터 테이블형태로 표현한것이 오른쪽 그림이다.
0행 0열부터 시작해서 7행 6열까지 표현할 수 있다.
이렇게 되면 비는 공간이 많아서 메모리 낭비가 생긴다.
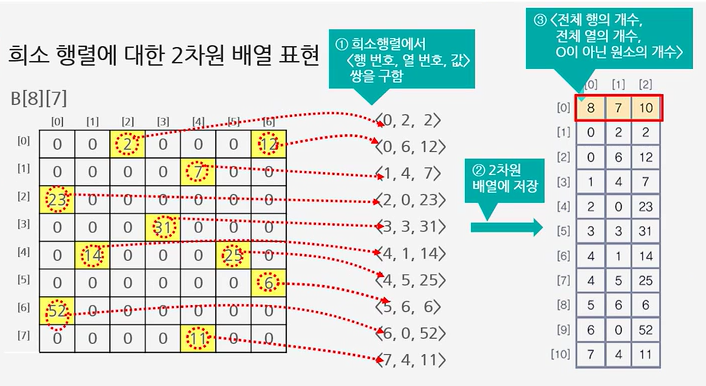
3. 희소 행렬에 대한 2차원 배열 표현
희소 행렬 B는 배열의 원소 56개 중 실제 사용하는 것은 0이 아닌 원소를 저장하는 10개뿐이므로
46개의 메모리 공간이 낭비된다
기억 공간을 좀 더 효율적으로 사용하기 위해 0이 아닌 값이 있는 원소만 따로 배열로 구성하는 방법
① 0이 아닌 원소만 추출하여 <행번호, 열번호, 원소> 쌍으로 배열에 저장한다.
② 추출한 순서쌍을 2차원 배열에 행으로 저장한다.
③ 원래의 행렬에 대한 정보를 순서쌍으로 작성하여 0번 행에 저장한다.
4. 희소행렬의 전치 연산 함수 프로그램

위에서 추출한 행렬의 행,열은 11행 3열이였다.
이것을 전치행렬로 바꿔주는 프로그램이다.
11*3 → 3*11
11행 3열을 → 3행 11열로 바꾼다.
typedef struct
구조체
int row, int col, int value
행, 열, 값

희소행렬의 첫번째 줄에는 행번호, 열번호, 원소값으로 이루어진다.
희소행렬 값을 저장하기 위한 구조체를 하나 만든것이다.

각각의 희소행렬의 a행의 갯수, a열의 갯수, 원소의 갯수
m, n, v에 넣었다.

전치행렬로 바꾸는 값
n, m, v를 0행에 넣어준다.

행우선을 열우선으로 표현하는 방법이다.

좀더 자세히 보자면 이런식이다.
실제 희소행렬의 전치 연산을 처리한것이다.
8행 7열 → 7행 8열

위 그림은 희소행렬을 메모리 절약한 유효한 값으로만 표현한 것을 전치행렬로 바꾸는 방법이다.
전치행렬은 행렬의 행과 열을 서로 바꿔 구성한 행렬이다.