이진 탐색 트리
이진 탐색 트리
| 이진 탐색 트리 | 데이터의 삽입, 삭제, 탐색 등이 자주 발생하는 경우에 효율적인 구조이며 최상위 레벨에 루트 노드가 있고 왼쪽 서브 트리에 있는 모든데이터는 현재 노드의 값보다 작고, 오른쪽 서브 트리에 있는 모든 노드의 데이터는 현재 노드의 값보다 크다. |
| 이진 탐색 트리에서 삽입 | 삽입할 위치는 루트 노드에서부터 시작되며 삽입할 노드의 데이터가 비교하는 노드의 데이터보다 작으면 왼쪽 서브 트리로 진행하고 크면 오른쪽 서브 트리로 진행한다. |
| 이진 탐색 트리에서 삭제 | 이진 탐색 트리에서 노드를 삭제하는 동작은 삭제할 노드의 위치에 따라 다른데 리프 노드인 경우와 삭제할 노드의 자식 노드가 하나인 경우, 삭제할 노드의 자식 노드가 구개인 경우에 따라 서로 다르게 처리한다. |
01. 이진 탐색 트리
1. 이진 탐색 트리
탐색 트리의 기본이 되는 트리이다.
데이터의 삽입, 삭제, 탐색 등이 자주 발생하는 경우에 효율적인 자료구조이다.
이진 탐색 트리는
이진 트리에 해당된다
이진 탐색 트리의 성질은
이진 트리이면서 같은 값을 갖는 노드가 없어야 한다.
# 이진 트리
최상위 레벨에 루트 노드가 있고 각 노드는 최대 두 개의 자식을 가진다.
왼쪽 서브 트리에 있는 모든 데이터는 현재 노드의 값보다 작고, 오른쪽 서브 트리에 있는 모든 노드의 데이터는 현재 노드의 값보다 크다.
즉, 현재 노드를 기준으로 왼쪽은 작고 오른쪽은 큰 값으로 구성이 되어있는 그런 트리이다.
이진 탐색 방법이 있었는데
이진 탐색은 데이터가 정렬이 되어있다는 전제하에 데이터의 비교하는 대상을 절반씩 줄여나가는 방식인데
이진 탐색 트리도 그것과 비슷하다.
2. 이진 탐색 트리의 예

첫 번째 트리
최대 자식 노드가 두 개 이면서, 루트를 기준으로 30을 기준으로 왼쪽 서브 트리는 다 30보다 작고, 오른쪽 서브 트리는 다 30보다 크다. 그리고 또한 20을 기준으로도 왼쪽 서브 트리는 20보다 작고, 오른쪽 서브 트리는 20보다 크다.
두 번째 트리
40을 기준으로 왼쪽은 40보다 작고, 오른쪽은 40보다 크다. 밑의 노드들도 다 그렇다.
세 번째 트리
23을 기준으로 왼쪽은 23보다 작고, 오른쪽은 23보다 크다. 밑의 노드들도 다 그렇다.
네 번째 트리
이것은 왼쪽으로 조금 치우진 트리라서 사향 이진 트리라고 더 많이 이야기한다.
완전한 사향 이진 트리는 아니지만, 왼쪽으로 조금 치우쳐져 있어 일반적으로 사향 이진트리라고 한다.
루트가 82이고, 82를 기준으로 왼쪽의 모든 노드들은 다 82보다 작다. 그리고 오른쪽을 보려고 하는데 오른쪽 노드는 없으므로 비교하지 않아도 된다. 밑의 노드들도 다 이진 탐색 트리 성질에 맞다.
3. 서브 트리의 예

서브 트리도 역시 이진 탐색 트리의 성질을 만족해야 하며
루트의 왼쪽 자식은 루트보다 작고 오른쪽 자식은 루트보다 크다.
4. 이진 탐색 트리에서의 탐색
데이터 탐색은
루트에서부터 시작된다.
루트 노드의 데이터와 찾으려는 데이터를 비교하여
루트 노드와 찾으려는 데이터가 같으면 탐색은 성공적으로 종료된다.
루트 노드의 데이터가 찾으려는 데이터보다 작으면
루트 노드의 오른쪽 서브 트리를 탐색해 간다.
루트 로드의 데이터가 찾으려는 데이터보다 크면
루트 노드의 왼쪽 서브 트리를 탐색해 간다
이진 탐색 트리는 이진 탐색의 연속이다.
한 번 비교할 때마다 왼쪽 서브 트리를 대상으로 할것인지, 오른쪽 서브 트리를 대상으로 할 것인지가 판단이 되기 때문에
비교해야 하는 데이터의 대상이 절반 가까이 줄어들게 된다.
이진 탐색 트리의 알고리즘

t 는
어떤 트리가 쭉 있으면 그 트리의 루트가 t가 된다.
x 는
내가 찾고자 하는 값이다.
| if (t=NIL or key[t]=x) then return t; |
t=NIL NIL은 leaf node이다. 더이상 자식이 없다라는 말이다. 더이상 자식이 없다라는 것은 끝까지 갔다라는 것이다. key[t]=x 현재 트리에 있는것들이 저장되어 있는 배열 key의 t에 있는 값과 x가 같으냐? then return t 그런 경우에는 t값을 리턴한다. |
| if(x < key[t]) then return treeSearch(left[t], x); else return treeSearch(right[t], x); |
(x < key[t]) x가 key의 t보다 작으면 then return treeSearch(left[t], x); t의 왼쪽 서브트리에 대해서 트리서치를 다시 한다. else return treeSearch(right[t], x); 작지않을경우 t의 오른쪽 서브트리에 대해서 트리서치를 다시 한다. treeSearch(t,x) 트리서치는 재귀호출, 자기 자신을 되부른다. |
5. 이진 탐색 트리에서의 탐색 예
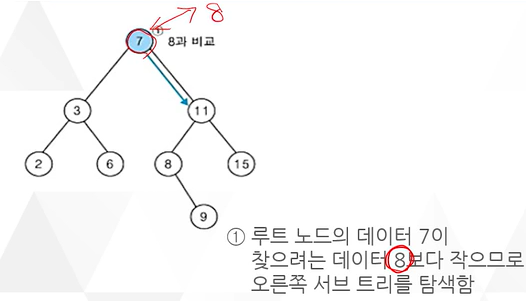


6. 이진 트리 탐색에서 재귀적 관점

이진 트리 탐색에서 루트 노드 t에서 왼쪽 자식 Left[t]로 분기하는 것은
Left[t]가 새로운 루트가 되었을 뿐 앞의 과정과 똑같은 작업이다.
즉, 루트 노드와 찾으려는 데이터의 대소 비교를 하고 나면
자신과 성격은 똑같으면서 더 작은 문제를 만난다. 우리가 이것을 재귀적이다. 재귀적인 알고리즘이라고 한다.
02. 이진 탐색 트리에서 삽입
1. 데이터 삽입
이진 탐색 트리에서의 삽입은
탐색 동작을 통해 이루어진다.
탐색에 성공하면 삽입은 실패한다.
이는 삽입하려는 데이터가 이미 존재한다는 의미인데 이진 탐색 트리는 같은 데이터를 갖는 노드가 없어야 한다.
탐색에 실패하면 삽입을 할 수 있으며
탐색이 종료된 지점의 데이터를 값으로 하는 노드가 삽입된다.
삽입할 위치는 루트 노드에서부터 시작되며
삽입할 노드의 데이터가 비교하는 노드의 데이터보다 작으면 왼쪽 서브 트리로 진행하고 크면 오른쪽 서브 트리로 진행한다.
예 ) 데이터가 30, 20, 25, 40, 10, 35의 순서로 원소가 삽입되는 경우 이진 탐색 트리가 만들어지는 과정
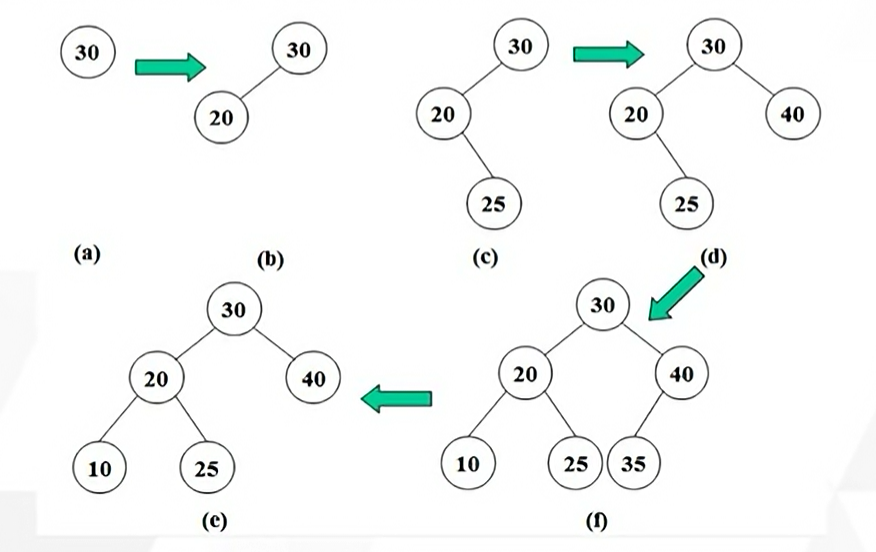
맨 처음 30이 들어왔을 때
30이 노드 하나이니깐 그냥 달린다.
그리고 20이 입력되었으면
20은 30보다 작으니깐 30의 왼쪽에 달리게 된다.
그다음 25가 입력되었으면
25는 루트하고 비교해서 30보다 작으니깐 왼쪽에 있어야 된다. 그리고 왼쪽 서브트리의 20과 비교했더니 20보다는 크므로 20의 오른쪽에 달려야 된다.
그다음 40이 입력되었다.
맨 위에 있는 루트와 비교해서 30과 40이 크기 비교를 한다. 40이 더 크므로 30의 오른쪽에 달려야 된다.
그다음 10이 들어왔다.
30과 10을 비교한다. 10이 30보다 작으니깐 왼쪽에 삽입되어야 한다.
그리고 20과 25가 있는 왼쪽 서브트리의 루트 20과 비교한다. 10이 20보다 작아서 20의 왼쪽에 달려야 된다.
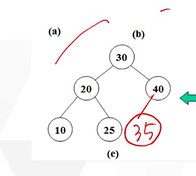
그다음 35가 입력되었다.
35는 또 루트 30과 비교된다. 35는 30보다 크니깐 오른쪽에 달리게 된다. 그리고 오른쪽의 40과 35를 비교하여 35가 더작기때문에 40의 왼쪽에 달리게된다.
이진 탐색 트리 데이터 삽입 알고리즘

2. 데이터 삽입의 예
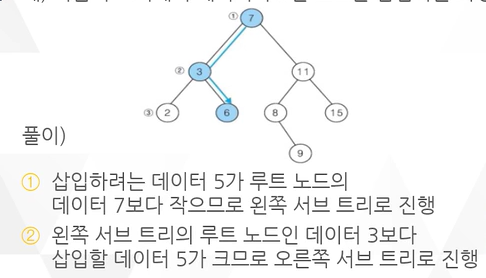
예 ) 다음의 트리에서 데이터가 5인 노드를 삽입하는 과정


3. 이진 탐색 트리의 특징
이진 탐색 트리는
좌우의 균형이 잘 잡힌 탐색 트리인데 균형이 잘 맞으면 탐색의 효율이 높다.
탐색 트리에서 효율은
트리의 깊이와 밀접한 관계가 있다.
트리의 모양이 극단적으로 왼쪽이나 오른쪽으로 치우쳐 있는 경우
탐색의 효율이 나쁘며 이것을 한쪽으로 치우쳐져있다. skewed(편향된) 했다. 해서 사향 이진 트리라고 부른다.
사향 이진 트리 (Skewed Binary Tree)
예를 들어 데이터가 10, 20, 25, 30, 40, 45의 순서로 원소가 삽입될 경우에 만들어지는 트리의 모양은 극단적으로 오른쪽으로 치우쳐 있다. (오른쪽 사향 이진 트리)
● 이 트리에서 45를 검색할 경우 10, 20, 25, 30, 40, 45의 순서로 트리의 모든 원소와 비교해야 한다.
● 40을 검색할 경우에는 10, 20, 25, 30, 40의 순서로 다섯 번의 비교가 필요하다. (검색 효율이 나쁘다.)
03. 이진 탐색 트리에서 삭제
1. 데이터 삭제
이진 탐색 트리에서 노드를 삭제하는 동작은
삭제할 노드의 위치에 따라 다음과 같이 세 가지로 구분되며 세 가지 경우에 따라 다르게 처리한다.
세 가지 경우

만약 case 1이면
r이 리프 노드라서 그냥 삭제해도 아무 영향이 없기 때문에 삭제한다.
만약 case 2 이면
r이 자식 노드가 왼쪽이나 오른쪽에 하나가 있다면 r이 삭제되고 그 빈 공간을 자식 노드가 당겨 올라온다.
만약 case 3 이면
문제는 r의 자식 노드가 둘일 때이다. 단말 노드 하나만 선택하면 남은 자식 노드가 상실이 된다. 그래서 이 경우 다른 기법이 필요하다.
이진 탐색 트리 데이터 삭제 알고리즘

case 3
삭제를 하고 난 다음에 트리를 재구성한다고 했을 때 이진 탐색 트리의 성질을 만족해야 된다.
그렇기 때문에
오른쪽 서브트리가 여러 개 있다고 한다면 그중에서 가장 작은 원소 노드 s를 삭제한다.
그리고 그 s는 올려져 r의 위치에 놓아진다.
2. 데이터 삭제의 예
Case 1 : r이 리프 노드인 경우
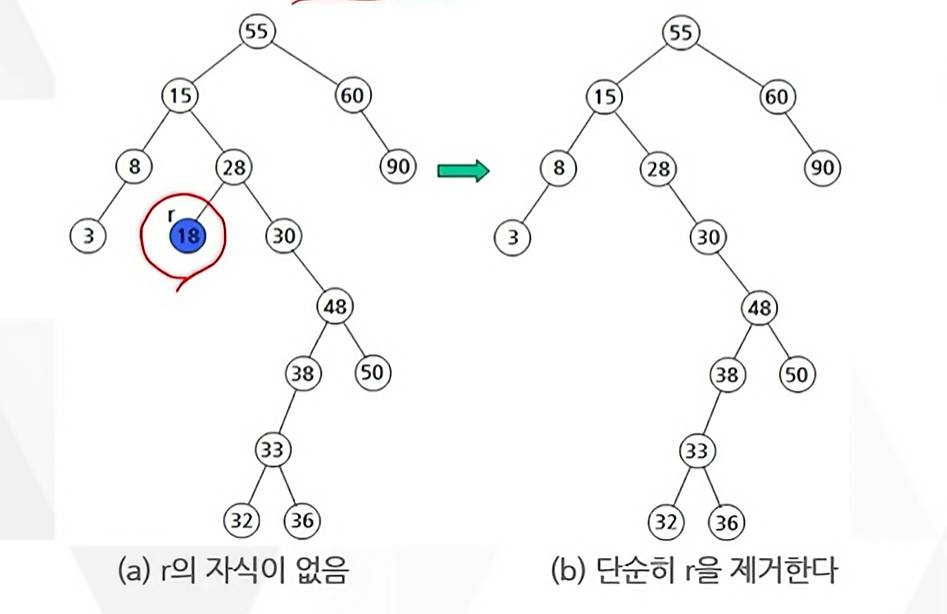
Case 2 : r의 자식 노드가 하나인 경우

Case 3 : r의 자식 노드가 두 개인 경우
자식이 두개인 경우가
조금 복잡하다.
r의 부모가 r을 가리키던 포인터는 하나인데
두 자식 중 하나만 이 포인터를 사용하고 나머지 하나는 연결을 끊을 수도 없다.
r을 삭제하더라도
r의 주변 구조는 그대로 유지해야 한다. 즉, 이진 탐색 트리의 성질을 만족해야 된다.
| 방법 | ① 우선 r 자리에 옮겨놓아도 이진 탐색 트리의 성질을 전혀 깨지 않는 원소를 찾는다. 왼쪽 서브트리에 있는 값을 하나 선택해서 r 자리에 옮겨놓아도 돼고, 오른쪽 서브 트리에 있는 값을 하나 선택해서 r 자리에 옮겨놓아도 된다. 단, 이진 탐색 트리의 성질을 깨트리지만 않으면 된다. ② 그런 원소는 왼쪽 서브 트리의 원소들보다 크고 오른쪽 서브 트리의 원소들보다 작아야 한다. 트리 전체에는 딱 2개가 있다. ● r의 왼쪽 서브 트리에서 가장 큰 원소 (크기 순으로 따지면 r의 직전 원소) 를 찾아서 r 자리에 옮겨놓는다. ● r의 오른쪽 서브 트리에서 가장 작은 원소 (크기 순으로 따지면 r의 직후 원소) 를 찾아서 r 자리에 옮겨놓는다. ③ 둘 중 하나를 택해 키를 r 자리로 옮긴다. 현재 예제에서는 직후 원소를 택한다. ④ 그런 다음 직후 원소가 들어 있던 노드를 삭제한다. 그러면 정상적으로 완료가 된다. |

28의 오른쪽 서브트리는 크게 구성되어 있지만
삭제하려는 이 r 노드의 자식노드는 왼쪽, 오른쪽 두 개이다.
r을 삭제하면 해당 자리는 비워지게 된다.
그러면 왼쪽에 있는 값, 오른쪽에 있는 값 중에서 r자리에 위치해도 이진 탐색 트리에 만족하는 숫자를 선택해서 올려줘야 된다.
그 데이터를 어떻게 찾느냐?
오른쪽에 있는 서브트리 중에서 가장 작은 값을 선택한다. 가장 작은 값은 30이다. 30을 r이 위치했던 곳으로 옮겨준다.
그러면 s 30이 있던 곳도 뻥 뚫려 없어지게 된다. s 노드는 자식노드가 한 개이므로
s 노드의 부모 노드 41과 38을 연결하면 된다.
삭제 작업의 수행시간
Case1과 Case2는
상수 시간이 든다.
Case3은
노드 r의 직후 원소를 찾는데 최악의 경우 트리의 높이에 비례하는 시간이 든다.
삭제 작업을 위한 최악의 시간은
트리의 높이에 따라 O(log n)과 O(n) 사이에 결정된다.
이진 탐색 트리에서의 탐색, 삽입, 삭제 연산의 시간 복잡도는
트리의 높이를 h라고 했을 때 O(h)가 된다.
따라서 n개의 노드를 가지는 이진 탐색 트리의 경우,
균형 잡힌 이진 트리의 높이는 log n이므로 이진 탐색 트리 연산의 평균적인 경우의 시간 복잡도는 O(log n)이다.