| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- 소프트웨어
- 출력
- 절차적 사고
- 공부정리
- 선택
- 미래 사회의 단위
- 겁나 많아
- 해결 방안
- 프로그래밍
- 반복 구조 찾기
- 뿌..
- 절차적 사고의 장점
- 레지스터
- 운영체제의 기능 1. 자원 관리 기능 2. 시스템 보호 3. 네트워크(통신 기능)
- 운영체제 목적
- 앨런 튜링
- 패킷트레이서 이용
- 말 인용
- 장치에 할당할 수 없는 NET ID Broadcast주소
- 순서도
- 운영체제의 미래
- 운영체제의 발달 과정
- 국립과천과학관
- 딥러닝
- 컴퓨터
- 소프트웨어 시대
- 운영체제 서비스
- 기계어
- 처리
- gensim 3.7.3 설치 오류
- Today
- Total
hye-_
플로이드 와샬 알고리즘 본문
| 플로이드 와샬 알고리즘 | 그래프에서 모든 정점 사이의 최단 거리를 구하기 위한 알고리즘이며 음수 가중치를 갖는 간선도 순환만 없다면 잘 처리되고 다익스트라 알고리즘보다 더 오래 걸리므로 문제 상황에 따라 적합한 알고리즘을 사용해야 한다. |
| 다익스트라 알고리즘 | 매번 가장 적은 비용을 가지는 노드를 하나씩 꺼내서 그 노드에 대해서 그 노드를 거쳐가는 비용을 확인하는 방법이며 어느 한 지점으로부터 모든 정점으로의 최단거리를 구하며 가중치가 양수일 때만 구할 수 있다. |
| 이행폐쇄 | 거쳐서 갈 수 있는 모든 곳을 직접 가는 간선으로 연결한 그래프이며 간선의 추가를 통해서 대부분의 노드들이 인접 노드로 바뀌게 되며 인접행렬로 표현하는 것이 편리하다. |
플로이드 와샬 알고리즘
최단 경로를 구하는 알고리즘인 플로이드 와샬 알고리즘은 가능한 모든 노드 쌍들에 대한 최단 거리를 구하는 알고리즘
○ 그래프에서 모든 정점 사이의 최단 거리를 구하기 위한 알고리즘
○ 동적 계획법 접근으로 그래프 상의 모든 두 정점을 잇는 경로의 최소 비용을 구함(여기에 경유지를 기록하면 최소 비용 경로까지 구할 수 있음
보통 플로이드 알고리즘이라고 불림
시간은 다익스트라 알고리즘에 비해 플로이드 와샬 알고리즘이 더 오래 걸리므로 문제 상황에 따라 적합한 알고리즘을 사용해야 함
한 정점에서 목적지 정점까지의 거리가 다른 정점들을 거쳐서 가는 가중치보다 크다면 거쳐서 가는 거리값을 저장해 나가는 방법
정점 A에서 B로 가는 경로와 정점 B에서 C로 가는 경로가 존재하면 A에서 C로 가는 경로도 존재한다고 할 수 있음
플로이드 알고리즘의 핵심 아이디어는 거쳐가는 정점을 기준으로 최단 거리를 구하는 것
○ 그래프 없이 인접 행렬만을 보고 이행 폐쇄를 결정하는 방법
○ 반복문 3개를 정점 수만큼 수행하기 때문에 시간 복잡도는 O(n^3) (3중 for문의 형태 사용)
○ 각 가중치에 대한 인접 행렬을 구해 놓고 시작
다익스트라 알고리즘과 플로이드 와샬 알고리즘 비교
| 다익스트라 알고리즘 | ○ 매번 가장 적은 비용을 가지는 노드를 하나씩 꺼내서 그 노드를 거쳐가는 비용을 확인 ○ 어느 한 지점으로부터 모든 정점으로의 최단 거리를 구함 ○ 가중치가 양수일 때만 구할 수 있음 |
| 플로이드 와샬 알고리즘 | ○ 거쳐가는 노드를 아예 반복문의 중심에 있도록 해서 문제를 해결하는 방법 ○ 애초에 거쳐가는 노드를 하나씩 다 설정해서 확인하는 방법 ○ 모든 정점에서 모든 정점으로의 최단거리를 구하는 것임 ○ 음수 가중치를 갖는 간선도 순환만 없다면 잘 처리됨 |

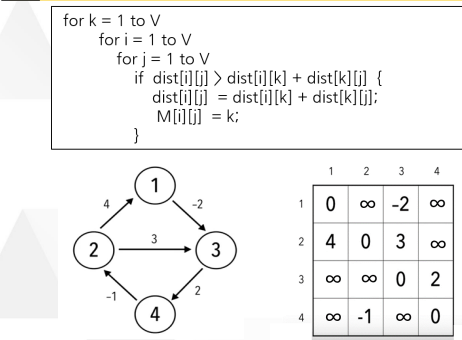
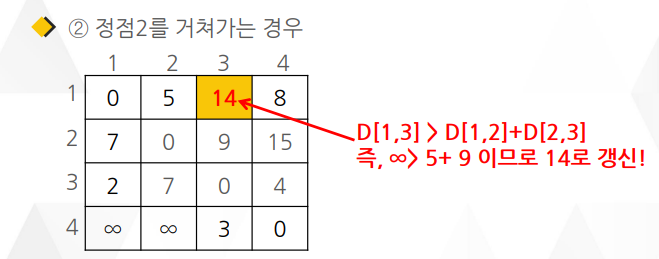
플로이드 와샬 알고리즘 예)

플로이드 와샬 알고리즘의 적용 방법
최단 경로 값을 저장하는 배열 dist[i][j]가 있다고 하자
dist[4][2]=10 이면 '정점4→정점2'까지의 최단 경로는 10임을 의미한다.
그런데 dist[4][1]=1, dist[1][2]=2라고 하면 '정점4→정점1'로의 경로값은 1이고 다시 '정점1→정점2'의 경로값은 2
따라서 '정점4→정점1→정점2'의 경로값은 총 3이 됨
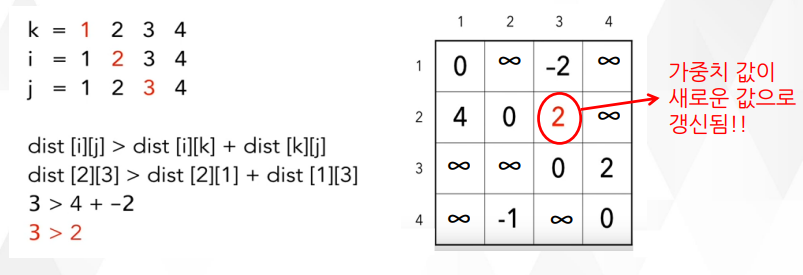
이는 기존에 저장된 dist[4][2]=10보다 작으므로 dist[4][2]=dist[4][1]+dist[1][2]
dist[4][2]=1+2=3이 되어 새로운 최단 거리 값이 저장됨
플로이드 와샬 알고리즘은 다음과 같은 접근으로 설계됨
○ 두 정점을 잇는 최소 비용 경로는 경유지를 거치거나 거치지 않는 경로 중 하나에 속함
○ 만약 경유지를 거친다면 그것을 이루는 부분 경로 역시 최소 비용 경로여야 함
○ 이는 중첩된 부분 문제로 볼 수 있으며 동적 계획법을 적용하여 효과적으로 접근할 수 있음
○ 한편 비용을 구하는 김에 어떤 경유지를 지나서 최소 비용을 만들었는지 기록해두면 최소 비용 뿐만 아니라 최소 비용 경로까지도 구할 수 있음



플로이드 와샬 알고리즘 수행시간
플로이드 와샬 알고리즘으로 모든 정점 간 경로의 최소 비용을 구하는 것은 O(|V|^3)의 시간
절대값을 쓴거나 안쓴거나 큰 차이는 없다. '갯수다'라는 것을 의미하기 위해서 절대값을 써준것이다.
그렇기에 O(V^3) 으로 쓸 수도 있고, O(n^3)이렇게 쓸 수도 있다.
경유지를 기록한 경우 경로를 역으로 추출하는 알고리즘의 복잡도는 O(|V|)의 시간 복잡도를 갖음
종종 다익스트라 알고리즘과 자주 비교되곤 하는데 두 알고리즘 모두 각각의 장단점이 있기 때문에 상황에 맞는 알고리즘 선정이 필요
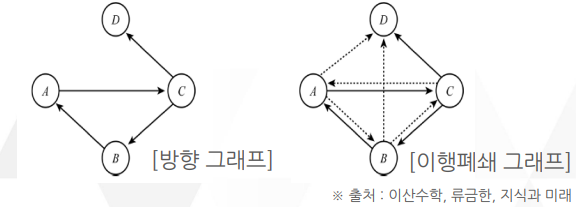
이행폐쇄 (Transitive Closure)
거쳐서 갈 수 있는 모든 곳을 직접 가는 간선으로 연결한 그래프
간선의 추가를 통해서 대부분의 노드들이 인접 노드로 바뀌게 되며 인접 행렬로 표현하는 것이 편리
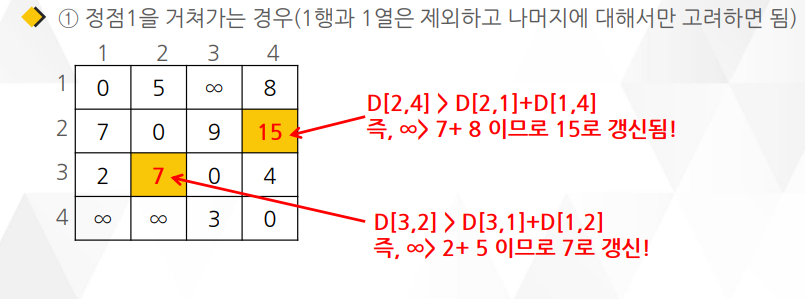
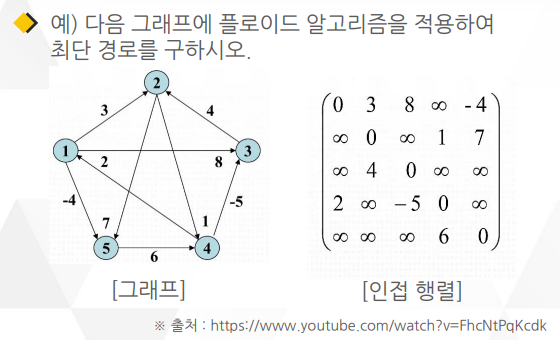
플로이드 와샬 알고리즘의 적용 예






'CS > 알고리즘' 카테고리의 다른 글
| 문자열 매칭 (오토마타, 라빈-카프알고리즘, KMP 알고리즘) (1) | 2024.07.14 |
|---|---|
| 그리디 알고리즘 (1) | 2024.07.14 |
| 다익스트라 알고리즘 (0) | 2024.07.12 |
| 최단 경로 (0) | 2024.07.12 |
| 위상 정렬 (0) | 2024.07.12 |




