| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- 순서도
- 해결 방안
- 뿌..
- 기계어
- 미래 사회의 단위
- 출력
- 국립과천과학관
- 프로그래밍
- 장치에 할당할 수 없는 NET ID Broadcast주소
- 운영체제의 미래
- 운영체제 서비스
- 처리
- gensim 3.7.3 설치 오류
- 절차적 사고
- 패킷트레이서 이용
- 운영체제의 발달 과정
- 운영체제 목적
- 말 인용
- 공부정리
- 겁나 많아
- 반복 구조 찾기
- 앨런 튜링
- 운영체제의 기능 1. 자원 관리 기능 2. 시스템 보호 3. 네트워크(통신 기능)
- 선택
- 레지스터
- 딥러닝
- 소프트웨어 시대
- 컴퓨터
- 소프트웨어
- 절차적 사고의 장점
- Today
- Total
hye-_
자료 정렬 방법 (셀 정렬, 히프 정렬, 트리 정렬) 본문
| 셀 정렬 | 일정한 간격(Interval)으로 떨어져있는 자료들끼리 부분 집합을 구성하고 각 부분 집합에 있는 원소들에 대해서 삽입 정렬을 수행하는 작업을 반복하면서 전체 원소들을 정렬하는 방법이다. |
| 히프 정렬 | 히프 자료구조를 이용한 정렬 방법이다. 히프에서는 항상 가장 큰 원소가 루트 노드가 되고 삭제 연산을 수행하면 항상 루트 노드의 원소를 삭제하여 반환한다. |
| 트리 정렬 | 이진 탐색 트리를 이용하여 정렬하는 방법이다. 트리 정렬 수행 방법으로 정렬할 원소들으 이진 탐색 트리로 구성하고, 이진 탐색 트리를 중위 우선 순회한다. 중위 순회 경로가 오름차순 정렬이 된다. |
셀 정렬(Sell sort)의 이해
일정한 간격(Interval)으로 떨어져있는 자료들끼리 부분집합을 구성하고 각 부분집합에 있는 원소들에 대해서 삽입 정렬을 수행하는 작업을 반복함녀서 전체 원소들을 정렬하는 방법
전체 원소에 대해서 삽입 정렬을 수행하는 것보다 부분집합으로 나누어 정렬하게 되면 비교연산과 교환연산 감소
셀 정렬의 부분집합
○ 부분집합의 기준이 되는 간격을 매개변수 h에 저장
○ 한 단계가 수행될 때마다 h의 값을 감소시키고 셀 정렬을 순환 호출
○ h가 1이 될 때까지 반복
셀 정렬의 성능은 매개변수 h의 값에 따라 달라짐
○ 정렬할 자료의 특성에 따라 매개변수 생성 함수를 사용
○ 일반적으로 사용하는 h의 값은 원소 개수의 1/2을 사용하고 한 단계 수행될 때마다 h의 값을 반으로 감소시키면서 반복 수행
정렬되지 않은 {69, 10, 30, 2, 16, 8, 31, 22}의 자료들을 셀 정렬 방법으로 정렬하는 과정
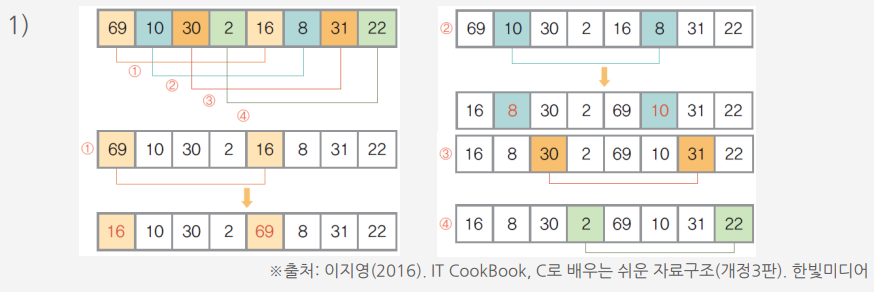
1) 원소 개수가 여덟개 이므로 매개변수 h는 4에서 시작한다. h=4이므로 간격이 4만큼 떨어져 있는 원소들을 같은 부분집합으로 만들면 네 개의 부분 집합이 만들어짐(같은 부분집합은 동일한 색으로 표시)
① 첫 번째 부분집합 {69, 16}에 대해서 삽입 정렬을 수행하여 정렬
② 두 번째 부분집합 {10, 8}에 대해서 삽입 정렬을 수행
③ 세 번째 부분집합 {30,31}에 대해서 삽입 정렬을 수행, 30<31이므로 자리 이동은 이루어지지 않음
④ 네 번째 부분집합 {2,22}에 대해서 삽입 정렬을 수행, 2<22이므로 자리 이동은 이루어지지 않음
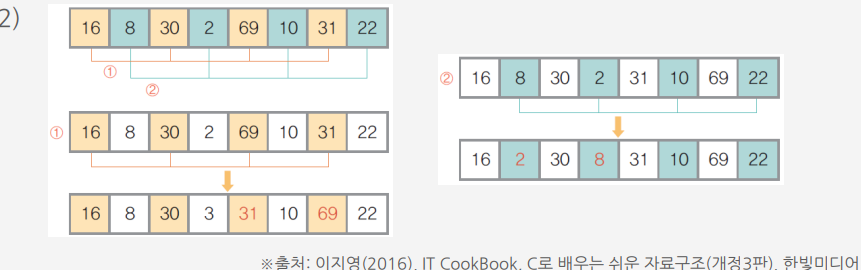
2) 이제 h를 2로 변경하고 다시 셀 정렬을 시작. h=2이므로 간격이 2만큼 떨어진 원소들을 같은 부분집합으로 만들면 두 개의 부분집합이 만들어짐
① 첫 번째 부분집합 {16, 30, 69, 31}에 대해 삽입 정렬을 수행하여 정렬
② 두 번째 부분집합 {8, 2, 10, 22}에 대해 삽입 정렬을 수행하여 정렬

3) 이제 h를 1로 변경하고 다시 셀 정렬을 시작. h=1이므로 간격이 1만큼 떨어져 있는 원소들을 같은 부분집합으로 만들면 한 개의 부분집합이 만들어짐, 즉 전체 원소에 대해서 삽입 정렬을 수행


병합 정렬 (Merge sort) 이해
여러 개의 정렬된 자료의 집합을 병합하여 한 개의 정렬된 집합으로 만드는 방법
부분집합으로 분할(Divide)하고, 각 부분집합에 대해서 정렬 작업을 완성(Conquer)한 후에 정렬된 부분집합들을 다시 결합(Combine)하는 분할 정복(Divide and conquer) 기법 사용
메모리 사용공간
각 단계에서 새로 병합하여 만든 부분집합을 저장할 공간이 추가로 필요
병합 정렬 방법의 종류
○ 2-way 병합 : 2개의 정렬된 자료의 집합을 결합하여 하나의 집합으로 만드는 병합 방법
○ n-way 병합 : n개의 정렬된 자료의 집합을 결합하여 하나의 집합으로 만드는 병합 방법
정렬되지 않은 {69, 10, 30, 2, 16, 8, 31, 22}의 자료들을 병합 정렬 방법으로 정렬하는 과정
2-way 병합 정렬 과정

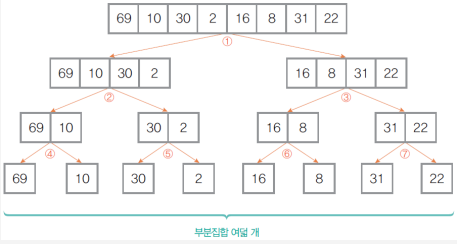
① 분할 단계
정렬할 전체 자료의 집합에 대해서 최소 원소의 부분집합이 될 때까지 분할 작업을 반복하여 한 개의 원소를 가진 부분집합 8개를 만듦
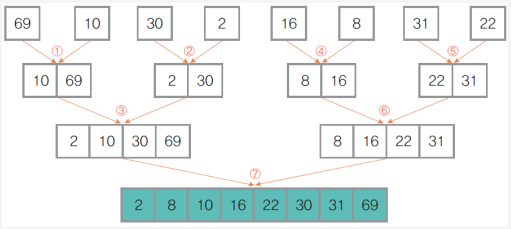
② 정복과 결합 단계
부분집합 두 개를 정렬하여 하나로 결합, 전체 원소가 집합 하나로 묶일 때까지 반복


히프 정렬(Heap sort)의 이해
히프에서는 가장 큰 원소또는 가장 작은 원소가 루트 노드가 되고 삭제 연산을 수행하면 항상 루트 노드의 원소를 삭제하여 반환
○ 최대 히프에 대해서 원소의 개수만큼 삭제 연산을 수행하여 내림차순으로 정렬 수행
○ 최소 히프에 대해서 원소의 개수만큼 삭제 연산을 수행하여 오름차순으로 정렬 수행
정렬되지 않은 {69, 10, 30, 2, 16, 8, 31, 22}의 자료들을 히프 정렬 방법으로 정렬하는 과정

1) 초기 상태
정렬할 원소에 대해 삽입 연산을 이용해 최대 히프를 구성
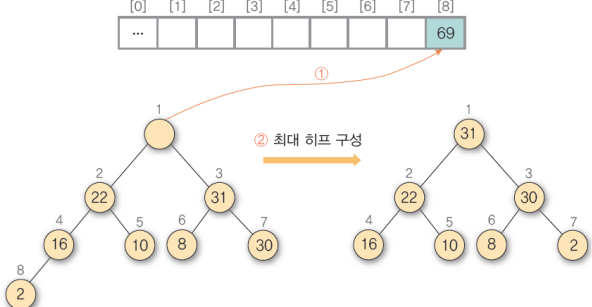
2) ① 히프에서 삭제 연산을 수행하여 루트 노드의 원소 69를 구한 후 배열의 마지막 자리에 저장 ② 나머지 히프를 최대 히프로 재구성
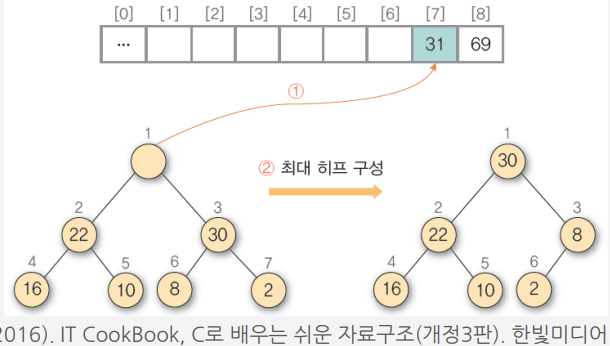
3) ① 히프에 삭제 연산을 수행하여 루트 노드의 원소 31을 구한 후 배열의 비어 있는 마지막 자리에 저장 ② 나머지 히프를 최대 히프로 재구성
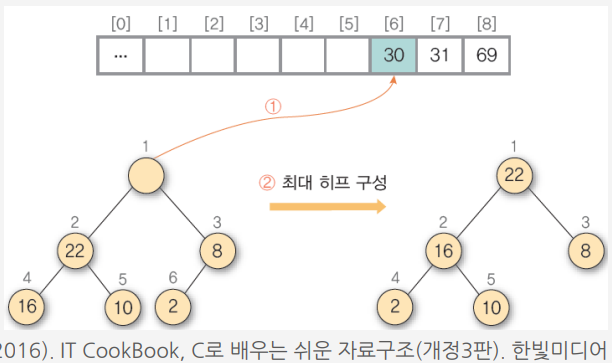
4) ① 히프에 삭제 연산을 수행하여 루트 노드의 원소 30을 구한 후 배열의 비어 있는 마지막 자리에 저장 ② 나머지 히프를 최대 히프로 재구성
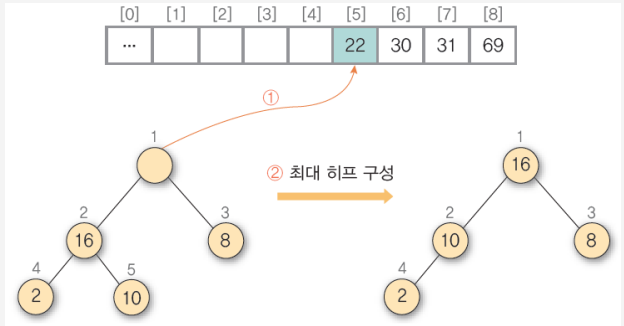
5) ① 히프에 삭제 연산을 수행하여 루트 노드의 원소 22를 구한 후 배열의 비어 있는 마지막 자리에 저장 ② 나머지 히프를 최대 히프로 재구성
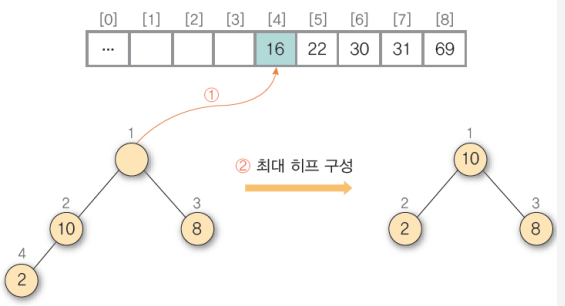
6) ① 히프에 삭제 연산을 수행하여 루트 노드의 원소 16을 구한 후 배열의 비어 있는 마지막 자리에 저장 ② 나머지 히프를 최대 히프로 재구성
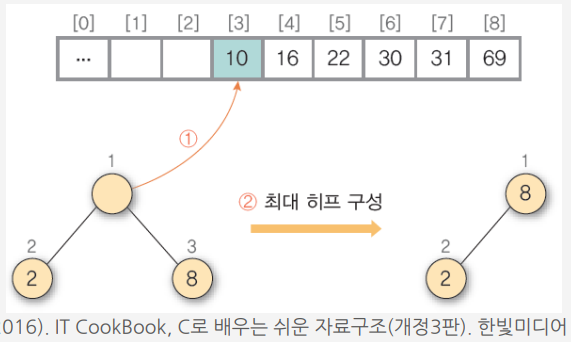
7) ① 히프에 삭제 연산을 수행하여 루트 노드의 원소 10을 구한 후 배열의 비어 있는 마지막 자리에 저장 ② 나머지 히프를 최대 히프로 재구성

8) ① 히프에 삭제 연산을 수행하여 루트 노드의 원소 8을 구한 후 배열의 비어 있는 마지막 자리에 저장 ② 나머지 히프를 최대 히프로 재구성

9) 히프에 삭제 연산을 수행하여 루트 노드의 원소 2를 구한 후 배열의 비어 있는 마지막 자리에 저장, 나머지 히프를 최대 히프로 재구성해야 하는데 공백 히프가 되었으므로 히프 정렬을 종료


트리 정렬 (Tree sort)의 이해
트리 정렬 수행 방법
○ 정렬할 원소들을 이진 탐색 트리로 구성
○ 이진 탐색 트리를 중위 우선 순회 함
○ 중위 순회 경로가 오름차순 정렬이 됨
정렬되지 않은 {69, 10, 30, 2, 16, 8, 31, 22}의 자료들을 트리 정렬 방법으로 정렬하는 과정
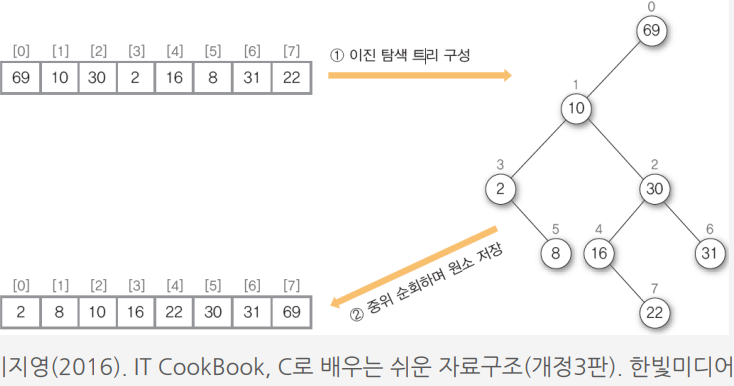
① 정렬할 원소 여덟 개를 차례대로 삽입하여 이진 탐색 트리를 구성
② 이진 탐색 트리를 중위 순회 방법으로 순회하면서 원소를 저장

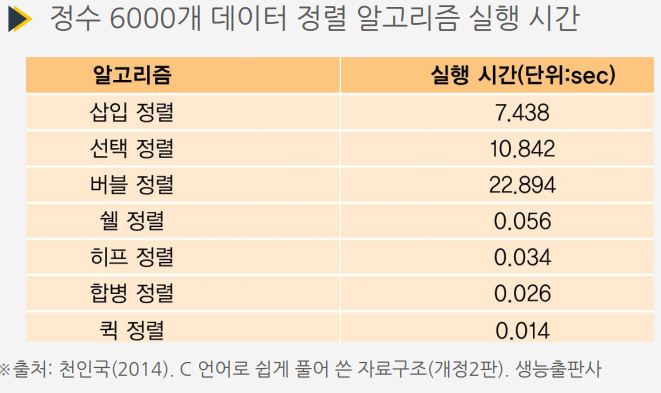
정렬 알고리즘 성능 비교

'CS > 자료구조' 카테고리의 다른 글
| 해싱 (동거자, 체이닝) (0) | 2024.07.08 |
|---|---|
| 검색 (순차검색, 이진 검색) (1) | 2024.07.08 |
| 자료 정렬 방법 (선택 정렬, 버블 정렬, 퀵 정렬, 삽입 정렬) (0) | 2024.07.06 |
| 그래프의 순회(깊이 우선 탐색, 너비 우선 탐색)와 신장 트리 (0) | 2024.07.05 |
| 그래프의 구조(그래프, 차수, 경로), 인접 행렬 (0) | 2024.07.05 |




