| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- 순서도
- 운영체제 서비스
- 운영체제의 기능 1. 자원 관리 기능 2. 시스템 보호 3. 네트워크(통신 기능)
- 운영체제의 발달 과정
- 절차적 사고
- 반복 구조 찾기
- 컴퓨터
- 뿌..
- 레지스터
- 장치에 할당할 수 없는 NET ID Broadcast주소
- 공부정리
- 소프트웨어
- 절차적 사고의 장점
- 패킷트레이서 이용
- 말 인용
- 소프트웨어 시대
- 운영체제 목적
- 처리
- 프로그래밍
- 미래 사회의 단위
- 운영체제의 미래
- 선택
- 앨런 튜링
- 딥러닝
- 국립과천과학관
- 기계어
- gensim 3.7.3 설치 오류
- 겁나 많아
- 출력
- 해결 방안
- Today
- Total
hye-_
그래프 개요 본문
| 그래프 | 현실세계의 복잡한 작업을 시각적으로 구조화하여 표현한 것으로 이해하기 쉽고 가시적으로 설명할 때 유용한 도구이며 현상이나 사물을 정점(Vertex)과 간선(Edge)으로 표현한 것이다. |
| 인접 행렬 | 그래프를 정점끼리의 인접 관계를 나타내는 행렬로 표현하는 방법인데 각 정점을 행과 열의 원소로 표현하여 두 정점을 연결하는 간선이 존재하면 행렬의 원소는 1, 존재하지 않으면 0으로 표현한다 |
| 인접 리스트 | 각 장점에 인접한 장점들을 순서에 상관없이 연결 리스트로 표현한 것이며 인접 리스트에서는 인접 행렬과는 달리 존재하지 않는 간선은 표현상 나타나지 않는다. |
그래프 (Graph)
현실세계의 복잡한 작업을 시각적으로 구조화하여 표현
○ 선형 자료 구조나 트리 자료 구조로 표현하기 어려운 다대다 관계를 가지는 원소들을 표현하기 위한 자료 구조
○ 이해하기 쉽고 가시적으로 설명할 때 유용한 도구
○ 현상이나 사물을 정점(Vertex)과 간선(Edge)으로 표현한 것
○ 주요 요소간의 관계, 거리, 비용 등 다양한 주제를 표현하고 설계할 때 유용
두 정점이 간선으로 연결되어 있으면 인접(Adjacent)하다고 함
간선은 두 정점의 관계를 나타냄
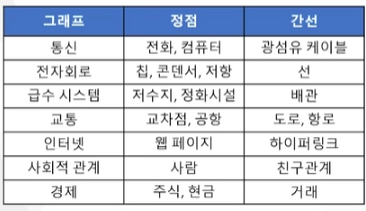
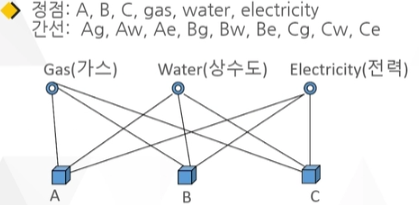
그래프의 예
1. 전국의 도로망, 도시의 지하철, 네트워크 구성도
2. 전산망, 인간 관계, 사회조직, 데이터 구조
3. 분자, 생물 유전자 관계 등

Graph G (V,E)
V : 정점 집합
E : 간선 집합

그래프의 기원
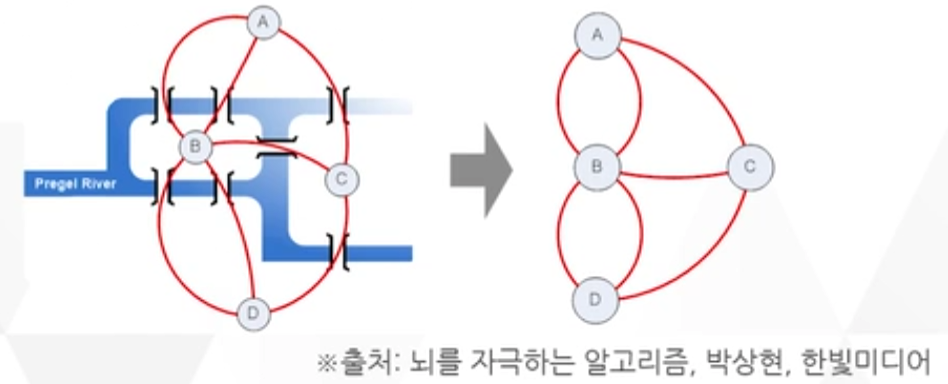
오일러가 쾨니히스베르크의 7개의 다리 문제를 풀기 위해 고안해 낸 수학적 도구
7개의 다리를 간선으로, 4개의 육지를 정점으로 표현
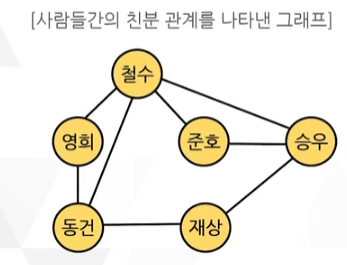

무향 그래프 (Indirected Graph)
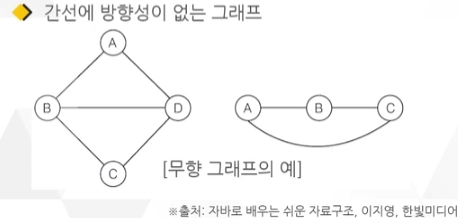
유향 그래프 (Directed Graph)

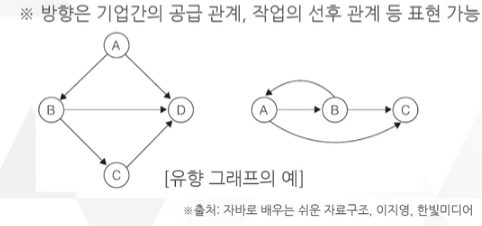

가중 그래프 (Weighted Graph)

그래프의 정점을 연결하는 간선마다 일정한 값을 할당한 그래프
간선에 할당하는 값은 각 정점 간의 거리나 비용과 같은 속성이 될 수 있음
예) 정점이 도시를, 간선이 건설할 도로를 나타낸다면 도로의 건설 비용을 간선의 가중치로 나타낼 수도 있음
그래프의 용어

① 인접 (Adjacent) : 간선으로 연결되어 있는 두 정점을 일컫는 말
이웃 관계에 있다고 표현하기도 함
② 경로 (Path) : 그래프에서 간선을 따라 갈 수 있는 길을 순서대로 나열한 것
○ 그래프 G1에서 정점 A에서 정점 C까지의 경로는 A-B-C, A-D-C, A-E-B-C등이 있음
○ A-B-C, A-D-C 경로의 길이는 2, A-E-B-C의 길이는 3임
③ 차수 (Degree) : 그래프에서 임의의 정점의 차수는 해당 정점에 연결된 간선의 개수
그래프에서 모든 정점의 차수의 총합은 모든 간선 개수의 2배
④ 부분 그래프 (Subgraph)
어떤 그래프를 구성하는 일부 정점과 간선으로만 구성된 그래프
⑤ 부분 신장 그래프 (Spanning Subgraph)
부분 그래프 중에서 그래프의 정점을 모두 포함한 부분 그래프
그래프의 표현 방법
그래프는 정점의 집합과 간선의 집합의 결합
○ 그래프를 표현하는 문제는 정점의 집합과 간선의 집합의 표현 문제로 생각할 수 있음
○ 간선은 정점과 정점이 인접 관계에 있음을 나타내는 존재
○ 그래프의 표현 문제는 간선, 즉 정점과 정점의 인접 관계를 어떻게 나타내는가의 문제임
행렬을 이용하는 방식은
인접 행렬(Adjacency Matrix)
리스트를 이용하는 방식은
인접 리스트 (Adjacency List)
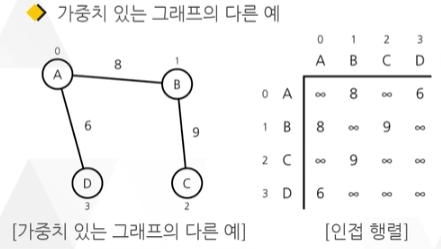
인접 행렬 (Adjacency Matrix)
그래프의 두 정점을 연결한 간선의 유무를 행렬로 저장
정점끼리의 인접 관계를 나타내는 행렬
각 정점을 행과 열의 원소로 표현
○ 두 정점을 연결하는 간선이 존재하면 행렬의 원소는 1, 존재하지 않으면 0으로 표현
○ 인접 행렬은 이해하기 쉽고 간선의 존재 여부를 즉각 알 수 있음
n*n 행렬로 표현 (n : 정점의 총 수)
원소 (i, j) = 1 : 정점i 와 정점j 사이에 간선이 있음
원소 (i, j) = 0 : 정점i 와 정점j 사이에 간선이 없음
n*n 행렬이 필요하므로 n^2에 비례하는 공간이 필요
행렬의 준비과정에서 행렬의 모든 원소를 채우는 데만 n^2에 비례하는 시간 필요
간선의 밀도가 아주 높은 그래프에서 인접 행렬이 적합
정점에 비해 간선이 적은 희소 그래프는 희소 행렬이 되어 메모리 낭비 발생




인접 리스트 (Adjacency List)
각 정점에 인접한 정점들을 순서에 상관없이 연결 리스트로 표현
○ 인접 리스트에서는 인접 행렬과는 달리 존재하지 않는 간선은 표현상 나타나지 않음
○ 그래프 내의 각 정점의 인접 관계를 표현하는 리스트
○ 각 정점의 차수만큼 노드를 연결
인접 리스트의 각 노드는 정점을 저장하는 필드와 다음 인접 정점을 연결하는 링크 필드로 구성
○ 정점의 헤드 노드는 정점에 대한 리스트의 시작을 표현
○ 가중치가 있는 그래프의 경우 리스트에 가중치도 보관함



인접 리스트는 공간이 간선의 총수에 비례하므로 인접 행렬에 비해 공간의 낭비가 없음
모든 가능한 정점 쌍에 비해 간선의 수가 적을 때 유용함
거의 모든 정점 쌍에 간선이 존재하는 경우 리스트를 만드는데 필요한 오버헤드가 더 많이 듦
인접 리스트는 간선의 밀도가 아주 높은 경우에는 적합하지 않음
인접 배열 (Adjacency Array)
인접 행렬과 인접 리스트는 장단점이 있음
연결이 촘촘하지 않아도 크기가 크면 인접 리스트를 사용하기가 어려움
왜냐하면 인접 리스트는 링크 필드가 있기 때문에 간선이 많지 않아도 정점의 수가 많아지면 인접 리스트로 표현하기 어렵기 때문이다.
두 정점간의 간선 존재 여부를 체크하는 일이 잦으면 수행 시간에 큰 부담을 줌
인접 리스트처럼 간선의 수에 비례하는 공간을 쓰면서 간선의 존재 여부를 훨씬 빨리 체크할 수 있는 방법이 인접 배열임
각 정점에 연결된 정점들을 연결 리스트로 저장하는 대신 배열로 저장하면
연결 리스트의 포인터를 관리하는 번거로움이 없어지고 두 정점의 인접 여부를 체크하는 시간도 줄일 수 있다.
n 개의 연결 배열로 표현할 수 있다.
○ i 번째 배열은 정점 i에 인접한 정점들의 집합
○ 가중치 있는 그래프의 경우 리스트에 가중치도 보관함

'CS > 알고리즘' 카테고리의 다른 글
| 트리 탐색 (너비 우선 탐색, 깊이 우선 탐색) (0) | 2024.06.23 |
|---|---|
| 오일러 사이클과 해밀턴 사이클 (0) | 2024.06.22 |
| 분할 정복 (0) | 2024.06.22 |
| 동적 계획법 (0) | 2024.06.22 |
| 해시 테이블의 충돌 해결 (체이닝, 개방 주소 방법[선형 조사,이차원 조사,더블 해싱]) (0) | 2024.06.22 |




