| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- 컴퓨터
- gensim 3.7.3 설치 오류
- 운영체제의 기능 1. 자원 관리 기능 2. 시스템 보호 3. 네트워크(통신 기능)
- 프로그래밍
- 공부정리
- 소프트웨어 시대
- 선택
- 운영체제 목적
- 운영체제의 발달 과정
- 절차적 사고의 장점
- 소프트웨어
- 순서도
- 미래 사회의 단위
- 운영체제 서비스
- 딥러닝
- 겁나 많아
- 장치에 할당할 수 없는 NET ID Broadcast주소
- 뿌..
- 국립과천과학관
- 기계어
- 레지스터
- 패킷트레이서 이용
- 말 인용
- 앨런 튜링
- 해결 방안
- 반복 구조 찾기
- 처리
- 출력
- 운영체제의 미래
- 절차적 사고
- Today
- Total
hye-_
탐색과 이진 탐색 본문
탐색과 이진 탐색
| 탐색 | 컴퓨터에서 자료를 찾는 방법을 의미하며 기억 공간에 보관 중인 데이터 중에서 원하는 정보를 찾아내는 작업이다. |
| 순차 탐색 | 순서화되어 있지 않은 경우 사용하며 첫 번째 데이터부터 차례로 비교하여 탐색하는 방식인데 파일이 크면 탐색 시간이 증가한다. |
| 이진 탐색 | 정렬된 데이터 집합을 이분화하면서 탐색하는 방법이며 정렬되어 있는 전체 파일을 두 개의 서브파일로 분리해가면서 키값을 검색한다. |
01. 레코드, 키의 정의 및 탐색 트리
1. 탐색 (검색)
컴퓨터에서 자료를 찾는 방법
기억 공간에 보관 중인 데이터 중에서 원하는 정보를 찾아내는 작업이다.
컴퓨터 안에는 엄청나게 많은 자료들이 있는데
컴퓨터는 자료를 빨리 찾을 수 있도록 일정한 논리 순서에 맞추어 작업을 한다. 이때 필요한 논리 순서가 탐색 알고리즘이다.
검색 엔진에서 키워드를 입력해 원하는 웹사이트에서 원하는 정보들을 검색한다.
이런 검색하는 과정을 탐색이다. 또는 검색이다.라고 한다.
책에서 어떤 내용을 찾기 위해 페이지를 마구 뒤지는 일
색인(Index)이 있으면 편리하게 책의 해당 페이지를 찾을 수 있다
엄청난 양의 웹 문서들을 빠른 시간에 검색해주는
구글과 같은 검색 엔진이 대표적인 탐색의 응용 예라고 할 수 있다.
탐색의 종류
순차 탐색, 이진 탐색 등이 있다.
적절한 자료구조와 알고리즘의 사용은
효율적인 데이터의 저장과 탐색에서 매우 중요하다.
데이터의 저장과 검색은
자료구조와 알고리즘에서 매우 중요하다.
데이터를 저장하는 효율적 자료구조가 개발되기 전에는
데이터가 들어오는대로 쌓는 방법밖에 없었다.
배열에 데이터가 들어오는 순서대로 쌓는 것은
데이터를 저장하기는 쉽지만 검색은 번거롭다.
이진 탐색 트리와 해시 테이블은
자료를 찾는 색인 역할을 하는 자료구조이다.
2. 레코드, 키, 탐색트리
(1) 레코드
레코드
개체에 대해 수집된 모든 정보를 포함하고 있는 저장 단위
예 ) 사람의 레코드라면
주민번호, 이름, 집주소, 연락처, 최종 학력, 이메일 등의 정보 포함

이 전체를 하나의 레코드라고한다.
테이블 형태로 표현한다고 하면
레코드는 행에 해당된다.
(2) 필드 (Field)
필드
레코드에서 각각의 정보를 나타내는 부분
예 ) 사람의 레코드에서
각각의 정보를 나타내는 부분이다. 즉, '주민번호'를 필드라고 한다.
테이블 형태로 표현한다고 하면
필드는 열에 해당된다.
(3) 탐색 키 (Search key) 또는 키 (Key)
탐색 키 또는 키
다른 레코드와 중복되지 않도록 각 레코드를 대표할 수 있는 필드
예 ) 사람 레코드의 경우
주민번호만 있으면 다른 사람 레코드와 구분될 수 있으므로 해당 레코드를 대표할 수 있다.
그렇기에 주민번호가 탐색 키가 될 수 있다.
키는 필드 하나로 구성할 수도 있고,
두 개 이상의 필드로 구성할 수도 있다.
예 ) 이름과 연락처를 사용하면
두 개의 필드로 구성된 키가 될 수 있다.
어떤 학교의 학생이 5천명이 있다. 5천 명의 학생 중에서 이름을 키로 할 수 있을까?
동명이인이 있을 수 있기 때문에 이름이 키가 될 수 없다.
만약 이름과 연락처 두개의 필드를 합치면 각 사람마다 다른 연락처를 갖고 있기 때문에 동명이인이라도 식별이 가능해진다.
(4) 탐색 트리 (Search Tree)
각 노드가 규칙에 맞도록 하나씩의 키를 갖고 있다.
이를 통해 해당 레코드가 저장된 위치를 알 수 있다.
저장되는 장소에 따라
내부 탐색 트리와 외부 탐색 트리로 나뉜다.
내부에 저장된다는 것은
주기억장치, 메인메모리에 저장이 된다는 것이다.
외부에 저장된다는 것은
보조기억장치에 저장이 된다.
| 내부 탐색 트리 | ● 탐색 트리가 메인 메모리 내에 존재한다. ● 메인 메모리에서 모든 키를 수용할 수 있으면 탐색 트리 전체를 메인 메모리로 한번만 탑재한 후 내부 탐색 트리로 사용할 수 있다. |
| 외부 탐색 트리 | ● 탐색 트리가 외부(주로 하드 디스크)에 존재한다. ● 메인 메모리에서 모든 키를 수용할 수 없을 정도로 크면 디스크 공간에 저장된 상태로 탐색해야 된다. |
02. 순차 탐색
1. 순차 탐색 (Sequential Search)
이해하기 쉽고 간단한 탐색 알고리즘
선형 탐색 (Linear Search)이라고도 한다. 한 줄로 나열이 되었다. 이런 개념으로 이해하면 된다.
순서화되어 있지 않은 경우 주로 사용하며
첫 번째 데이터부터 차례대로 비교하여 탐색하는 방식이다.
원하는 데이터를 찾을 때까지
키를 하나씩 비교해 가는 방식이다.
어떤 학생이 천명 있는데, 홍길동을 찾고으면
1번부터 그 사람이 홍길동인지를 1000번까지 찾는다.
데이터가 정렬되어 있을 때도 하나씩 비교하면서 원하는 값을 찾기 때문에 비효율적이다.
홍길동을 찾을 때 'ㅎ'으로 시작하는 것부터 찾으면 되는데 처음부터 하나씩 다 비교하니 비효율적이다.
파일이 크면
탐색 시간이 증가한다.
예
무작위로 모여진 명함 중에서 원하는 사람의 명함을 찾는 경우 앞에서부터 찾는다.
시간 복잡도
O(n)
왜 O(n) ?
전체가 100개일 때 1부터 100까지 순서대로 찾아야 되니깐 n만큼의 시간이 걸린다.
최악의 경우 홍길동이 100번에 있을 경우 100번까지 비교를 해야 되기 때문이다.
최선의 경우에는 홍길동을 찾는데 1번에 있을 때이다. 1번만 비교를 하여 찾을 수 있다.
2. 순차 탐색 방법
예 ) 데이터 집합에서 순차 탐색을 이용해 데이터 3을 탐색하는 과정

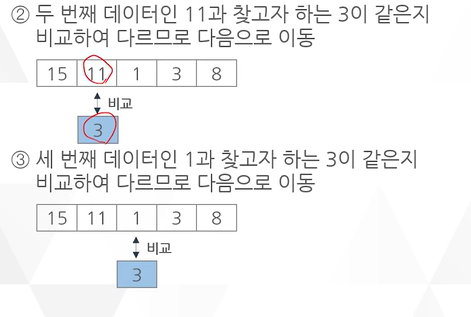
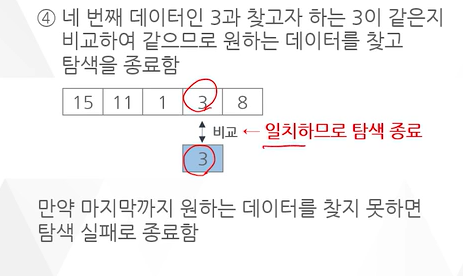
3. 자기 구성 순차 탐색 (Self-Organizing Sequential Search)
순차 탐색을 하기 위해서 어떤 방법이 있느냐?
자기 구성 순차 탐색의 방법이 있다. 이것은 순차 탐색 방법을 조금 더 개선한 방법이라고 할 수 있다.
자주 사용되는 항목을 데이터 집합의 앞쪽에 배치함으로써
순차 탐색의 검색 효율을 끌어올리는 방법
내가 빈번하게 자주 이용하는 데이터라고 한다면
앞에 부분 몇 번 비교하다 보면 내가 원하는 데이터를 찾을 수 있다.
이렇게 구성하는 방법을 자기 구성 순차 탐색이라고 한다.
책꽂이에 몇백 권이 꽂혀있다. 그중에서 내가 자주 보는 책을 접근하기 쉬운 위치에 배치하게 되면 빨리 찾을 수 있다.
크게 3가지 방법이 있다.
1. 전진 이동법 (Move To Front)
2. 전위법 (Transpose)
3. 빈도 계수법 (Frequency Count)
(1) 전진 이동법 (Move to front)

어느 항목이 한번 탐색이 되고 나면
그 항목을 데이터 집합의 가장 앞에 위치시키는 방법이다.
내가 만약 48을 한번 탐색했다면
무조건 48을 가장 앞에 위치시킨다.
(2) 전위법 (Transpose)

탐색된 항목을
바로 이전 항목과 교환한다.
전진 이동법과는 달리
자주 사용되면 사용될수록 점진적으로 해당 항목을 데이터 집합의 앞쪽으로 이동시키는 방법이다.
(3) 빈도 계수법 (Frequency count)
데이터 집합 내의 각 요소들이 탐색된 횟수를 별도의 공간에 저장해 두고
탐색된 횟수가 높은 순으로 데이터 집합을 재구성한다.
계수 결과를 저장하는 별도의 공간을 유지해야 하고
계수 결과에 따라 데이터 집합을 재배치해야 한다.
03. 이진 탐색
1. 이진 탐색 (Binary Search)
정렬된 데이터 집합을 이분화하면서 탐색하는 방법이다.
정렬되어 있는 전체 파일을 두 개의 서브파일로 분리해 가면서 키값을 검색한다.
예
가나다순으로 정렬되어 있는 전화번호부에서 임의 사람에 대한 전화번호를 찾는 경우
찾고자 하는 키값을
파일의 중간 레코드 키값과 비교하면서 검색한다.
전체 데이터가 있으면 내가 찾고자 하는 데이터와 중간 데이터와 같은지 비교한다.
같지 않고 내가 찾고자하는 데이터가 더 크다
그렇다면 오름차순으로 정렬되어 있다 가정하에 중간데이터 오른쪽의 절반 데이터에서 다시 이진탐색을 반복한다.
시작과 끝의 인덱스를 설정하고
그 중간값을 구한 후 키와 중간값을 계속 비교하면서 검색한다.
파일의 탐색 시간을 1/2씩 줄여가면서 탐색하므로 효율적이다.
레코드의 수가 많을수록 효과적이다.
중간 레코드 번호를 계산하는 방법

m middle(중간)
전체 데이터중에서 가운데 레코드를 일단 찾아서 비교한다

m은 2분의 low(아래)와 upper(위)
위아래를 더해서 반으로 나눈 중간값은 m이다.
시간 복잡도
O(logn)
대상이 절반씩 줄어든다.
정렬된 데이터 집합에서 사용할 수 있는 '고속' 탐색 알고리즘

2. 이진 탐색의 작동 예
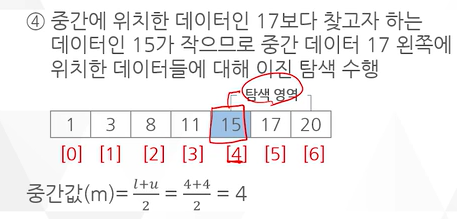
예 ) 다음의 정렬된 데이터 집합에서 이진탐색을 이용해 데이터 15를 탐색하는 과정
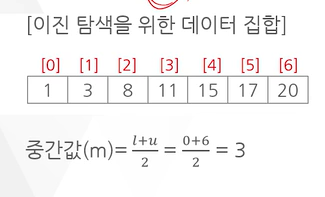
low가 0이고, upper가 6이다 그러면 m은 2분의 0+6인 3이다.
인덱스가 3인 11과 내가 찾고자 하는 15와 비교한다.


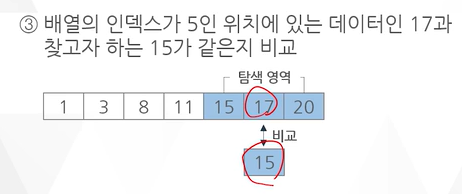

'CS > 알고리즘' 카테고리의 다른 글
| 레드 블랙 트리 (0) | 2024.06.20 |
|---|---|
| 이진 탐색 트리 (0) | 2023.12.09 |
| 특수한 정렬 알고리즘 (힙 정렬, 기수 정렬, 계수 정렬) (0) | 2023.11.24 |
| 효율적인 정렬 알고리즘 (쉘 정렬, 병합 정렬, 퀵 정렬) (0) | 2023.11.22 |
| 기본적인 정렬 알고리즘 (선택 정렬, 버블 정렬, 삽입 정렬) (0) | 2023.11.10 |




